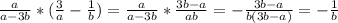
Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔ 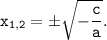
Тогда
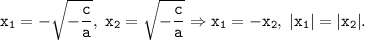
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.