Объяснение:
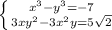
сложим эти два уравнения и преобразуем по формуле куба разности:

Для простоты вычислений введём константу С
![C=\sqrt[3]{5\sqrt{2}-7 }](/tpl/images/2018/3457/220b9.png)
C≈0,4142
Из последнего выражения имеем следующие тождества
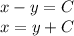
Подставляем x в первое уравнение
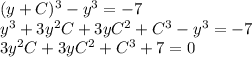
В последнее С³ подставим его значение, чтобы сократить семёрку.
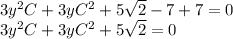
Теперь решаем обычное квадратное уравнение
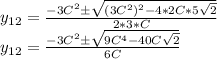
Тут получается что дискриминант отрицательный и корней нет.
Вариант второй, графический
из первого уравнения получаем график функции
![y=\sqrt[3]{x^{3} +7} \\](/tpl/images/2018/3457/4771c.png)
А из второго
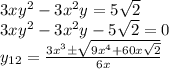
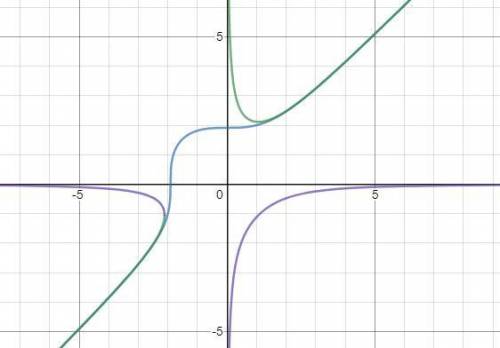
Строим графики.
Видим, что точек пересечения нет.
Графики стремятся приблизится друг к другу, но не пересекаются
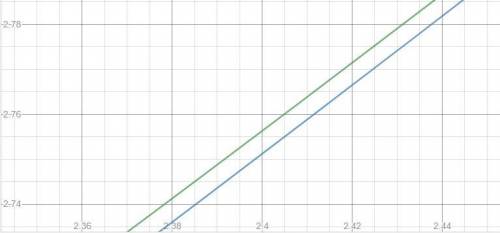
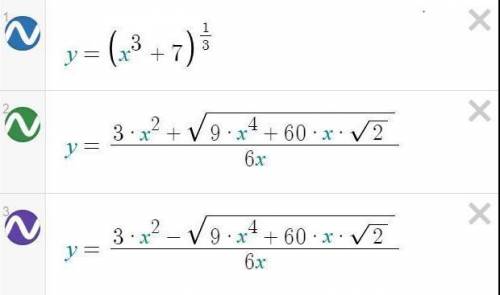
У нас есть правильный многоугольник. Поставим внутрь его точку, и проведем от этой точки отрезки ко всем углам многоугольника.
В итоге многоугольник разделится на треугольники.
Смотрим рисунок, на нем правильный 6-угольник.
Треугольников всегда будет столько же, как углов у многоугольника.
Сумма углов в каждом треугольнике равна 180°.
Сумма уголов во всех n треугольниках равна (180*n)°.
Сумма углов вокруг начальной точки (красная окружность) равна 360°.
Сумма углов многоугольника равна (180*n - 360)° = 180(n - 2)°
Так как многоугольник правильный, то все углы одинаковые.
Каждый угол равен 180(n - 2)/n. По условию он равен 108°.
180(n - 2)/n = 108
180(n - 2) = 108n
180n - 360 = 108n
180n - 108n = 360
n = 360/(180 - 108) = 360/72 = 5