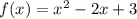
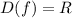

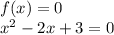


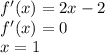
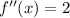
а² – b² = 2017
а² – b² = (а – b) * (а + b)
(а – b) * (а + b) = 2017
Число 2017 простое, поэтому имеет только два натуральных делителя 1 и 2017.
2017 = 1 * 2017
Поэтому
(а – b) * (а + b) = 1 * 2017
Имеем систему
{а + b = 2017
{а – b = 1
Из второго уравнения получим
а = b + 1
Подставим в первое уравнение
(b + 1) + b = 2017
2 b = 2017 - 1
2 b = 2016
b = 2016 : 2
b = 1008
а = 1008 + 1 = 1009
Проверка чисел а = 1009; b = 1008
1009² – 1008² = 2017
1018081 – 1016064 = 2017
2017 = 2017
ответ: существует только 1 вариант натуральных чисел разность квадратов которых равна числу 2017. Это числа 1008 и 1009.
1 проехал S=v1*15 => v1=S/15
2 проехал S = v2*(t+4) => v2=S/(t+4)
В тоже время S= v1t+v2t= t(v1+v2) S=t[(S/15)+S/(t+4))]
S=tS(1/15+1/t+4)
1=t/15+t/(t+4)
15(t+4)=t^2+4t+15t
15t+60=t^2+4t+15t
t^2+4t-60=0
t=-10 не может быть
t=6
ответ 6 часов