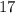 и
и  – среднеарифметическое равно
– среднеарифметическое равно  и при этом
и при этом  на
на  меньше двадцати пяти и на
меньше двадцати пяти и на  больше семнадцати.
больше семнадцати. монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на  монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на  монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на 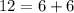 монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.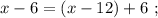
 монет, а у Пети-II будет
монет, а у Пети-II будет  монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в 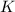 раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 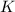 раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:

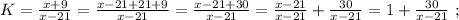

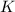 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 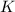 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 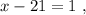 откуда:
откуда:
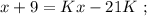

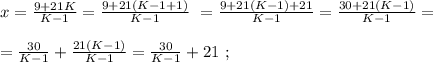
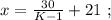
 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 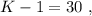 откуда:
откуда:
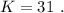
Решение сводится к нахождению вершины параболы (см.ниже).
Для начала, из уравнения
x+2y=6
выразим игрек:
y=3-0,5x
И подставим это выражение в произведение xy.
Получим такую функцию:
f(x) = xy = x(3-0,5x) = -0,5x²+3x
Эта функция показывает, как меняется значение произведения xy при изменении переменной икс (и, соответствующего ему изменения игрек, ведь они связаны указанным в задаче уравнением).
График этой функции- это парабола, ветви которой уходят вниз. А верхняя точка (максимум)- это вершина параболы.
Координату икс вершины можно вычислить как среднее арифметическое между иксами в нулях функции.
Нули функции (точки, в которых функция равна нулю) будут при:
x₁=0 и 3-0,5x = 0, то есть при x₂=6
Среднее равно x₀=(0+6)/2=3
При этом, функция будет равна:
f(3) = -0,5*3²+3*3 = 4,5
Это и есть наше искомое максимальное значение произведения xy.
ответ: 4,5

26-8x=0⇒8x=26⇒x=26/8=13/4∈[2;14]
y(2)=-2*e^5≈296,8-наиб
y(13/4)=0,5*e^0=0,5
y(14)=22*e^-43=0-наим