1. (х+4)(х+6) 2. (х -3)(х -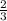 
)
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 =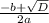 
находим первый корень, который равен -4
А с формулы х2=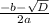
находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 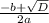находим первый корень, который равен 3
А с формулы х2=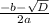 находим второй корень, который равен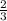
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )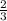
1. (х+4)(х+6) 2. (х -3)(х - )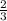
Объяснение:
1. х^2 +10x - 24
a=1, b=10, c=-24
Находим дискриминант и получаем D= 4
формулы x1 = 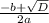находим первый корень, который равен -4
А с формулы х2=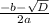 находим второй корень, который равен -6
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)
2. 3x^2-11x+6
a=3, b=-11, c=6
Находим дискриминант и получаем D= 49
формулы x1 = 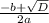находим первый корень, который равен 3
А с формулы х2=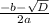 находим второй корень, который равен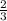
Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)
Получаем:
3x^2-11x+6= 1(x-3)(x- )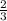
cosx-√3/2=0
cosx=√3/2
x=плюс минус π/6 + 2πn,n∈Z
Это решение уравнения. Ищем корни,для этого подставляем это решение в промежуток от [0;3 пи].
0≤плюс минус π/6 + 2πn≤3π
переносим пи деленное на 6 влево и вправо,выражаем n:
так как мы брали n только четные,минус пропадал,то решений нет.
Аналогично повторяем со второй частью,только n берем нечетные,т е в решении минус сохраняется:
тоже нет решений. Итог:это уравнение не имеет решений либо просто оно неверно написано.