Пусть это число А, так как оно окончивается цифрами 17 и делится на 17 (17 делится на 17), то представив число А в виде A=100B+17, где B - некоторое неотрицательное целое число. Видим что A-17=100B+17-17=100B должно делится на 17, так как 100 на 17 не делится, то число В должно делится на 17. При данных условиях оно должно быть наименьшим, и сумма цифр должна ровнять 17-1-7=9
Так как сумма цифр числа В равна 9, то оно делится на 9(а так как оно делится еще на 17), НОК(9, 17)=9*17=153, значит число В равно 153, а данное число равно
15317
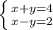



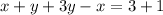

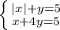
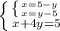
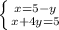

PO = (1; 3) - (-2; -1) = (3; 4)
O (3; 4)