Р пр-ка = 60 м
Sдор. = 64 м²
шир. дор. = ? м
Решение.
Если а и b - длина и ширина, соответственно, м, то
Рпр-ка = 2а + 2b ---- периметр здания
х, м ---- ширина дорожки
Площадь дорожки складывается из 8 участков, Двух равных по длине длине здания, двух равных по длине ширине здания и четырех квадратов по углам, со стороной равной стороне дорожки.
Sдор. = 4х² + 2ах + 2bх = 4х² + х(2а + 2b) = 4х² + х*Рпр-ка
4х² + 60х = 64 ----- по условию | : 4
х² + 15х - 16 = 0
D = 15² + 4*16 = 225 + 64 = 289 = 17²
х₁ =(-15 + √17²)/2 = (-15+17)/2 = 1 (м) ----- ширина дорожки
х₂ = (-15 - 17)/2 = - 16 м -- отбрасываем, как посторонний корень, не имеющий физического смысла
ответ: 1 м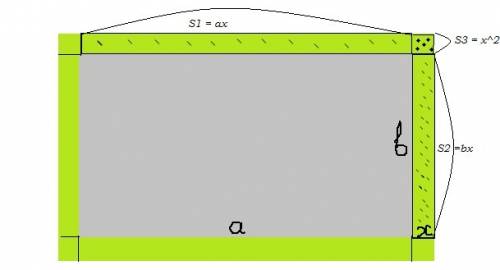
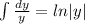
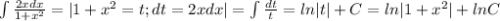
Два варианта прочтения условия:
===========================================