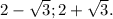
Объяснение:
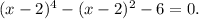
Пусть 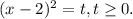 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
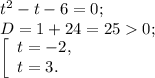
Условию 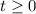 удовлетворяет t=3. Значит
удовлетворяет t=3. Значит
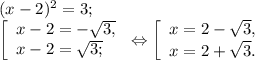
d=18-16=2
Найдем последний 30-й член прогрессии по формуле an=a1+d(n-1):
а30=16+2*29=84
Т.к. максимальный член больше 70, то в этой прогрессии встретим числа 38 и 70, но не встретим 53, т.к. разность прогрессии - четное число и первый член прогрессии - четное число.
Найдем, какими по порядку членами являются числа 38 и 70 (из формул выше).
16+2(n-1)=38
2n-2=38-16=22
2n=22+2=24
n=12, т.е. число 38 - 12-й член прогрессии
16+2(n-1)=70
2n-2=70-16=54
2n=54+2=56
n=28, т.е. число 70 - 28-й член прогрессии
(x - 2)⁴ - (x - 2)² - 6 = 0
(x - 2)² = t - новая переменная
(x - 2)² = 3 или (x - 2)² = -2
x² - 4x + 4 - 3 = 0 корней нет
x² - 4x + 1 = 0
D = (-4)² - 4 * 1 * 1 = 16 - 4 = 12
ответ: 2 ± √3