Question

Найдите все значения параметра а, при которых система имеет единственное решение.

Answer 1

Заметим, что если пара (x₀, y₀) – решение системы, то и пара (x₀, -y₀) также является решением системы. Доказывается это подстановкой -y вместо y в уравнения:

В первом уравнении рассмотрим только первые две скобки:

$(3-2\sqrt{2})^{-y}+(3+2\sqrt{2})^{-y}=\frac{1}{(3-2\sqrt{2})^{y}}+\frac{1}{(3+2\sqrt{2})^{y}}=\frac{(3+2\sqrt{2})^{y}}{(3-2\sqrt{2})^{y}(3+2\sqrt{2})^{y}}+\\+\frac{(3-2\sqrt{2})^{y}}{(3+2\sqrt{2})^{y}(3-2\sqrt{2})^{y}}=\frac{(3+2\sqrt{2})^{y}}{(3^2-(2\sqrt{2})^2)^y}+\frac{(3-2\sqrt{2})^{y}}{(3^2-(2\sqrt{2})^2)^y}=\frac{(3+2\sqrt{2})^{y}}{1^y}+\frac{(3-2\sqrt{2})^{y}}{1^y}=\\=(3+2\sqrt{2})^y+(3-2\sqrt{2})^y$

После замены y на -y сумма не изменилась, значит, уравнение осталось тоже неизменным.

Во втором уравнении при подстановке -y минус «съедается» квадратом, поэтому уравнение также остаётся неизменным.

Исходя из этого единственным решение бывает тогда, когда y = -y, то есть y = 0. Получаем такую систему:

$\begin{equation*}\begin{cases}2-3a=x^2+6x+5,\\(a^2-5a+6)x^2=0,\\-6\leq x\leq 0\end{cases}\end{equation*}$

Рассмотрим функцию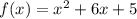 $f(x)=x^2+6x+5$ на промежутке -6 ≤ x ≤ 0. Вершина этой параболы находится в точке с абсциссой -3, ось симметрии ровно посередине заданного промежутка. Значит, при x = -3 парабола принимает ровно одно значение, а при всех остальных заданных x – ровно два. Отсюда единственность решения достигается:

1) x = -3 (единственное решение первого уравнения), причём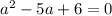 $a^2-5a+6=0$, иначе не будет решений второго уравнения;

2) x = 0 (единственное решение второго уравнения).

Случай, когда первое уравнение имеет два решения, а второе – только одно из них, не достигается.

Случай 1 (x = -3):

$2-3a=(-3)^2+6*(-3)+5 \Leftrightarrow 2-3a=-4 \Leftrightarrow a=2$

При таком a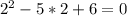 $2^2-5*2+6=0$ - верно, значение подходит.

Случай 2: (x = 0):

$2-3a=0^2+6*0+5 \Leftrightarrow 2-3a=5 \Leftrightarrow a=-1$.

Проверка значений параметра на посторонние решения:

При a = 2 из второго уравнения следует, что y = 0, тогда из первого следует, что $x^2+6x+5=-4$, это уравнение также имеет единственное решение.

При a = -1 первое уравнение имеет вид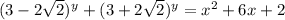 $(3-2\sqrt{2})^y+(3+2\sqrt{2})^y=x^2+6x+2$. Рассмотрим функции 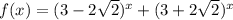$f(x)=(3-2\sqrt{2})^x+(3+2\sqrt{2})^x$ и $g(x)=x^2+6x+2, -6\leq x\leq 0$.

$f'(x)=((3-2\sqrt{2})^x+(3+2\sqrt{2})^x)'=((3-2\sqrt{2})^x)'+((3+2\sqrt{2})^x)'=\\=(3-2\sqrt{2})^x\ln{(3-2\sqrt{2})}+(3+2\sqrt{2})^x\ln{(3+2\sqrt{2})}=\\=(3+2\sqrt{2})^x\ln{(3+2\sqrt{2})}-(3-2\sqrt{2})^x\ln{(3+2\sqrt{2})}=\\=\ln{(3+2\sqrt{2})}((3+2\sqrt{2})^x-(3-2\sqrt{2})^x)$

Нули производной:

$\ln{(3+2\sqrt{2})}((3+2\sqrt{2})^x-(3-2\sqrt{2})^x)=0\\(3+2\sqrt{2})^x=(3-2\sqrt{2})^x\\x=0$

Функция убывает при x ≤ 0 и возрастает при x ≥ 0. Значит, x = 0 – точка глобального минимума. Минимальное значение функции f(0) = 2. Значит, E(f) = [2; +∞).

g(x) – парабола. При заданных ограничениях E(g) = [-4; 2]. Значит, решение первого уравнения существует, если:

$\left \{ {{f(y)=2} \atop {g(x)=2}} \right. \left \{ {{y=0} \atop {x=-6; 0}} \right.$

Вид второго уравнения при a = -1: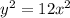 $y^2=12x^2$. Пара решений (-6; 0) не является его решением. Пара (0; 0) является его решением. Значит, система имеет единственное решение.

ответ: -1; 2