Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2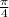
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2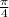) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
Т.к. f(t) = (t - 2)^2 - 4 имеет минимум в t = 2, а функция sqrt(x) непрерывна и монотонно возрастает на всей области определения и 2 входит в область значений, то точка, в которой sqrt(x) = 2, является точкой минимума.
x = 4 - точка минимума.
Путь для запрограммированных роботов:
f'(x) = 1 - 2/sqrt(x) = 0
sqrt(x) = 2
x = 4
В точке x = 4 производная меняет знак с минуса на плюс, так что x = 4 - точка минимума.