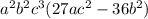
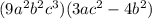
пусть данная дробь a/(a+2), тогда обратная дробь (a+2)/a, и новая дробь
(а+2-3)/а=(а-1)/а
получаем уравнение:
(а-1)/а - а/(а+2) = 1/15
переносим 1/15 влево и приводим к общему знаменателю
Для удобства я знаменатель писать не буду, он будет 15а(а+2). Пишу только числитель:
15(а+2)(а-1)-15а^2-a(a+2)
15a^2-15a+30a-30-15a^2-a^2-2a=0 (потому что дробь равно 0 тогда, когда числитель равен 0, а знаменатель не равен 0, значит имеем ввиду, что а не может быть равно 0,1 и -2) и ищем, когда числитель равен 0:
-a^2+13a-30=0
D=169-120
D=49
а=(-13+-7)/-2
а=10 ; 3
10 нам не подходит, поскольку по условию исходная дробь - несократимая, значит она не может быть 10/12, значит ответ: 3/5
х²-4х+7х-28-9+х²+32≥0
2х²+3х-5≥0
2х²+3х-5=0
D=b²-4ac=9+40=49
x1=-b+√D/2a=-3+7/4=4/4=1
x2=-b-√D/2a=-3-7/4=-10/4=-2.5
+ - +
-2.51>
ответ: (-бесконечности; -2,5] в объединении [1;+бесконечности)