Теорема о медианах треугольника
Рассмотрим произвольный треугольник АВС.
teorema_o_medianah_treugolnikama – медиана треугольника, проведенная к стороне BC
mb – медиана треугольника, проведенная к стороне AC
mc– медиана треугольника, проведенная к стороне AB
O – центр пересечения медиан треугольника
A, B, C – вершины треугольника
Теорема о медианах треугольника формулируется следующим образом: медианы треугольника пересекаются в одной точке (на рисунке точка O) и делятся этой точкой в пропорции 2:1, если считать от вершины, с которой проведена медиана.
Все формулы по теме теорема о медианах треугольника:
Основные формулы
Формулы площадей
Формулы объемов
Формулы периметра
Геометрические фигуры
Объемные тела
Площадь поверхности
Тригонометрические формулы
Теоремы по геометрии
Теорема Пифагора
Обратная теорема Пифагора
Теорема косинусов
Теорема синусов
Теорема тангенсов
Теорема о медианах треугольника
Теорема о биссектрисе
Теорема о сумме углов треугольника
Теорема о сумме углов многоугольника
Теорема Чевы
Теорема Виета
Теорема Фалеса
Первое задание
Число делится на 4, если число, составленное из последних двух цифр, делится на 4. В данном случае это 37628 (ведь 28 делится на 4).
ответ: 37628.
Второе задание
Преобразуем это число по правилам действий со степенями:
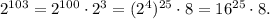
Число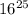 
оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что 
).
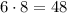ответ: на 8.
Третье задание
Преобразуем выражение по правилам действий со степенями:
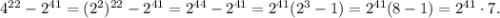
ответ: на 7.
***
Если будут какие-нибудь вопросы — задавайте.
Если мой ответ оказался полезен, отмечайте его как «лучший ответ».
!x! достигает минимума при 0 и далее возрастает до бесконечности
2^!x! соответствеено от 1 до +00