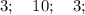
Объяснение:
6) Так как произведение корней принимает положительное значение, то и сами корни принимают положительные значения ⇒ подкоренные выражения также положительны.
ОДЗ:
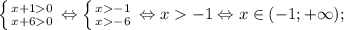
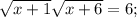
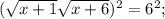
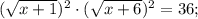
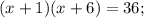
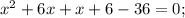
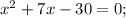
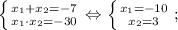
Корень x₁ не удовлетворяет ОДЗ.
7) Знаменатель дроби не равен нулю ⇒ подкоренное выражение строго больше 0. Подкоренное выражение правой части уравнения также строго больше 0, поскольку, в противном случае, значение числителя равно 0, отсюда выходит, что "х" принимает отрицательное значение, что противоречит ОДЗ подкоренного выражения знаменателя дроби.
ОДЗ:
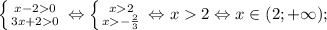
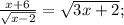

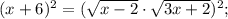

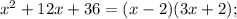
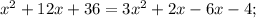
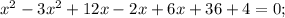
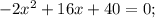
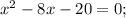
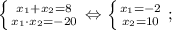
Корень x₁ не удовлетворяет ОДЗ.
8) ОДЗ:

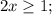
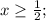
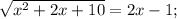
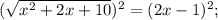
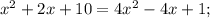
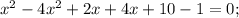
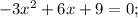
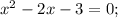
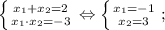
Корень x₁ не удовлетворяет ОДЗ.
-3x - x = -1 - 0.2
-4x = -1.2
x = -1.2 : (-4)
x = 0.3
y = 0.3 - 1 = - 0.7
(0.3, -0.7)