Рассмотрим две функции g(x) = x и f(x) = arcsin x.
g(x) = x - линейная, строго монотонно возрастающая, нечётная непрерывная функция, D(g) = R. График - прямая линия, проходящая через начало координат.
f(x) = arcsin x - обратная тригонометрическая, строго монотонно возрастающая, нечётная непрерывная функция, D(f) = [-1; 1]. График - кривая линия, проходящая через начало координат.
Оба графика проходят через начало координат (0;0).
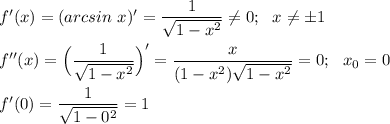
Прямая y=x - касательная к графику функции f(x) = arcsin x в точке перегиба x₀=0, то есть графики пересекаются только в этой точке.
ответ : уравнение имеет единственный корень x=0
6x-15-24 =< 12-4x
20x+4 > 20-5x
10x =< 51
25x > 16
x =< 5,1
x > 0,64
x ( 0,64 ; 5,1 ]
2.
40-4-6-15x < 10-6x
40x+20 >= 30+70x-40-32x
-9x < -20
2x >= -30
x > 2,2
x >= -15
x ( 2,2 ; +бесконечность)