Объяснение:
1.
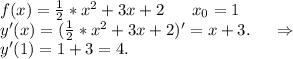
ответ: y'(1)=4.
2.

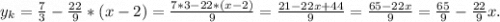
3.
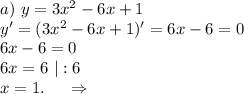
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(-∞;1) функция убывает.
При х∈(1;+∞) фунуция возрастает .
![b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1](/tpl/images/1848/3010/401ca.png)
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
При х∈(-∞;-1) фунуция возрастает .
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(1;+∞) функция возрастает. ⇒
При х∈(-1;1) функция убывает.
Объяснение: у=7/х- обратная пропорциональность,
график- гипербола. Область определения: х ≠0
Область значений: у≠0
таблица значений х 0,5 1 2 7 -0,5 -1 -2 -7
у 14 7 3,5 1 -14 -7 -3,5 -1
На координатной плоскости в 1-ой и в 3-ей четвертях постройте по точкам из таблицы график из 2-х кривых под названием гипербола. Обе кривые относятся к одному графику и никогда не пересекают оси ох и оу, а только приближаются к ним.
С графиком у=5/х надо отработать аналогично. Желаю успеха.
.по теореме Виета х₁+х₂=4 х₁*х₂= - 12, х₁=6 х₂= -2
2
. через Дискриминант
Д=(√7+√2)²-4*√14=7+2√14+2-4√14=9-2√14
выделив полный квадрат (9-2√14)= (√7-√2 )²⇒ √Д = √7-√2
х₁= (√7+√2-√7+√2)\ 2 = √2
х₂ = (√7+√2+√7-√2)\ 2 = √7
3. по теореме Виета х₁+х₂=10 х₁*х₂=-24 х₁=12 х₂=-2
4. через Дискриминант
Д=19²-4*3*16= 169
√Д=√169=13, х₁=(19-13)\6= 6\6=1 х₂= (19+13)\6 = 32\6 = 16\3
5. 3х²-6х+х-2 - 4х²+12х-9-х²+4х-4=0 ⇒2х²-11х+15=0 ⇒ Д=11²-4*2*15=1⇒√Д=1
х₁=(11-1)\4 = 10\4 = 5\2 х₂=(11+1)\4 = 3