Упростите (cos(22°-α)-cos(18°+α))²+(cos(68°-α)+sin(72°-α))²
Объяснение: информация для размышления
sin(90 -α) =cosα ; cos(90-α) = sinα ; cos(α-β)=cosα*cosβ+sinα*sinβ
(A ± B)² =A²±2A*B +B)²
!?
1. (cos(22°-α) - cos(18°+α))²+(cos(68°- α)+sin(72°-α))² =
(cos(22°-α)- cos(18°+α))²+(cos(90° -(22°+α))+sin(90°-(18°+a))² =
(cos(22°-α)- cos(18°+α))²+(sin(22°+α)+cos(18°+a) )² =
cos²(22°-α)- 2cos(22°-α)*cos(18°+α)+cos²(18°+α) +
sin²(22°+α)+2sin(22°+α)*cos(18°+a)+ cos²(18°+a) =
!!
2. (cos(22°-α) - cos(18°+α))²+(cos(68°+ α)+cos(72°-α))² =
(cos(22°-α)- cos(18°+α))²+(cos(90° -(22°-α))+cos(90°-(18°+α))² =
(cos(22°-α)- cos(18°+α))²+(sin(22°-α)+sin(18°+α) )² =
cos²(22°-α)- 2cos(22°-α)*cos(18°+α)+ cos²(18°+α) +
sin²(22°-α)+2sin(22°- α)*sin(18°+α) + sin²(18°+α) =
( cos²(22°-α)+sin²(22°-α)) -2(cos(22°-α)*cos(18°+α)- sin(22°- α)*sin(18°+a) )+
( cos²(18°+α) +sin²(18°+a) ) =1 -2cos(22-α+18+α) +1 =2 -2cos40°=
2(1 -cos40°) =2*2sin²20° = 4sin²20 .
! ! !
3. (cos(32°-α) - cos(28°+α))²+(cos(58°+ α)+cos(62°-α))² =
(cos(32°-α)- cos(28°+α))²+(cos(90° -(32°-α))+cos(90°-(28°+α))² =
(cos(32°-α)- cos(28°+α))²+(sin(32°-α)+sin(28°+α) )² =
cos²(32°-α) - 2cos(32°-α)*cos(28°+α)+ cos²(28°+α) +
sin²(32°-α) + 2sin(32°- α)*sin(28°+α) + sin²(28°+α) =
( cos²(32°-α)+sin²(32°-α)) -2(cos(32°-α)*cos28°+α)- sin(32°- α)*sin(28°+a) )+
( cos²(28°+α) +sin²(18°+a) ) =1 -2cos(32-α+28+α) + 1 = 2 -2cos60°=
2-2*1/2= 1
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
2(1 -cos60°) =2*2sin²30° =4sin²30 = 4*(1/2)² =4*1/4 =1
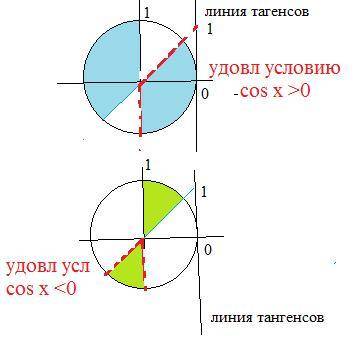
Eсли cosx > 0, т. е х в 1 и 4 четверти, делим на cosx
tgx < 1⇒ -(π/2)+πk < x < (π/4)+πk, k∈Z
Неравенству удовлетворяют корни, для которых соsx>0
Получаем
-(π/2)+2·πk < x < (π/4)+2·πk, k∈Z
Eсли cosx < 0, т. е х в 2 и 3 четверти, делим на cosx
tgx > 1⇒ (π/4)+πn < x < (π/2)+πn, n∈Z
Неравенству удовлетворяю корни, для которых соsx>0
Получаем
(3π/4)+2·πn < x < (π/2)+2·πn, n∈Z
О т в е т. Объединение ответов:
((π/2)+2·πk ; (π/4)+2·πk) U (3π/4)+2·πn ; (π/2)+2·πn), k, n∈Z
х+1 км/ч скорость 1-го велосипедиста,
240/х - 240/х+1 =1, х≠0, х≠-1,
240(х+1)-240х=х(х+1),
240х+240-240х=х²+х,
х²+х-240=0,
D= 1-4*1*(-240)=1+960=961,
√D=31
х=(-1+31)/2=15
х=(-1-31)/2=-16 меньше 0, не является решением задачи, поэтому 15 км/ч скор 2-го велосипедиста, а 15+1=16 (км/ч) скорость 1-го велосипедиста.
ответ: 16 км/ч.