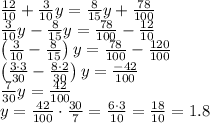
Объяснение:
|x -1| + |x +3| ≤ 4
Решим это неравенство методом интервалов.
Найдем нули подмодульных выражений:
х - 1 =0 → х = 1
х + 3 = 0 → х = - 3
Эти значения разбивают числовую ось на три интервала:
х ∈ (-∞; - 3] ; (-3; 1]; (1; + ∞)
Решим заданное неравенство на каждом из этих промежутков.
1) 1) x∈ (-∞; - 3], при этом неравенство примет вид:
- (х - 1) - (х + 3) ≤ 4
-х + 1 - х - 3 ≤ 4
-2х ≤ 6
х ≥ - 3
Пересекая найденное решение x∈ [- 3; +∞) c рассматриваемым интервалом x∈ (-∞; - 3] , получаем решение x = - 3
2) х ∈ (-3; 1]
- (х - 1) + х + 3 ≤ 4
0*х ≤ 4 → х - любое число. Учитывая интервал, х х ∈ (-3; 1]
3) х ∈ (1; + ∞)
х - 1 + х + 3 ≤ 4
2х ≤ 2
х ≤ 1 → х ∈ (- ∞; 1]
Для получения окончательного ответа объединим полученные решения:
x ∈ [- 3] ∪ (-3; 1] ∪ (- ∞; 1]
ответ: х ∈ [-3; 1]
При решении этих неравенств надо понимать, что графиком квадратичной функции является парабола. Ветвями вверх или вниз. Если хорошо понимать, как проходит парабола,легко поставить знаки квадратичной функции и потом ответить на вопрос задания.
а) х² - 6х +8 > 0
Корни 2 и 4
-∞ (2) (4) +∞
+ - + знаки квадратичной функции
решение неравенства
ответ: х∈(-∞;2)∪(5;+∞)
б) х² + 6х +8 < 0
корни -2 и -4
-∞ (-4) (-2) +∞
+ - + знаки квадратичной функции
решение неравенства
ответ: х∈(-4; -2)
в) -х² -2х +15 ≤ 0
корни -5 и 3
-∞ [-5] [3] +∞
- + - знаки квадратичной функции
решение неравенства
ответ: х∈ (-∞; -5]∪ [3; + ∞)
г) -5х² -11х -6 ≥ 0
корни -1 и -1,2
-∞ [-1,2] [-1] +∞
- + - знаки квадратичной функции
решение неравенства
ответ: х ∈ [-1,2; -1]
д) 9x² -12x +4 > 0
D = 0 корень один
х = 2/3
-∞ (-2/3) +∞
+ + знаки квадратичной функции
решение неравенства
ответ: х∈ (-∞; 2/3)∪ (2/3; +∞)
е) 4х² -12х +9 ≤ 0
D = 0, корень один х = 3/2
-∞ [3/2] +∞
+ + знаки квадратичной функции
∅
3/10у-8/15у=0,78-1,2
-7/30у=-0,42
у=-0,42:(-7/30)
у=1,8