Исследовать на сходимость ряд 
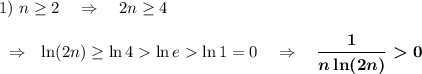
Следовательно,  положительный числовой ряд.
положительный числовой ряд.
2) Чтобы ряд сходился, необходимо (но не достаточно), чтобы его общий член стремился к нулю :

3) Интегральный признак Коши :
Если несобственный интеграл 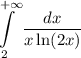 сходится (в результате вычислений получится число), то будет сходиться числовой ряд
сходится (в результате вычислений получится число), то будет сходиться числовой ряд  .
.
Если несобственный интеграл 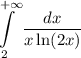 расходится (в результате вычислений получится бесконечность), то будет расходиться числовой ряд
расходится (в результате вычислений получится бесконечность), то будет расходиться числовой ряд  .
.
4) Подынтегральная функция непрерывна на интервале [2;+∞).
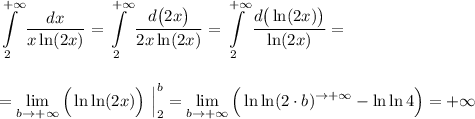
ответ : ряд расходится