a) D(x) = (-∞; +∞)
б) D(x) = (-∞;0) U (0;+∞)
Объяснение:
Область определения функции - это те значения аргумента (х), при которых СУЩЕСТВУЕТ функция.
Другими словами, если вы хотите найти область определения функции, то это значит найти значения х.
В наших случаях:
а)
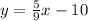
Это линейная функция. Аргумент (х) не имеет ограничений (не стоит в знаменателе , под знаком корня).
Поэтому : x - любое число, или
D(x) = (-∞; +∞)
б)
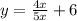
В этой функции мы видим х в знаменателе. Значит функция будет существовать при всех значениях аргумента (х), кроме 0, т.е
5х≠0
х≠0
получаем:
D(x) = (-∞;0) U (0;+∞)
Решение задачи № 3.
1. Разделим обе части уравнения на а, чтобы оно стало приведенным (т.е. коэффициент а должен равняться 1). Имеем:
2. По теореме Виета: произведение корней приведенного квадратного уравнения равняется его свободному члену, т.е. коэф. с. Имеем:
Подставляя значение первого корня -3 и сокращая, имеем:
ах=2
3. По теореме Виета: сумма корней приведенного квадратного уравнения равняется второму коэфф., взятому с противоположным знаком. Имеем:
Подставляя значение первого корня -3 и сокращая, имеем:
ах=2а+1
4. Имея одинаковые левые части полученных уравнений, приравниваем их правые части:
2=2а+1
2а=1
а=1/2
5. Зная а и подставляя его в уравнение ах=2, находим второй корень:
1\2х=2
х=2*2
х=4
ответ. Второй корень равен 4.