Объяснение:
чтобы построить графики функций, вместо а подставим различные значения
а=0
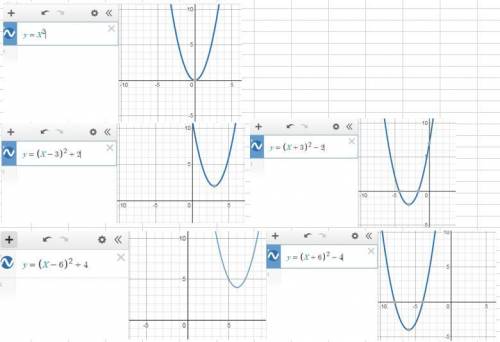
тогда функция получается такая: y=x²
а=1
функция y=(x-3)²+2
а=2
функция y=(x-6)²+4
а=-1
функция y=(x+3)²-2
а=-2
функция y=(x+6)²-4
Можно взять 2 или 3 функции, но пусть будет больше для ясности
Теперь построим графики этих функций. Все они - параболы, т.к. x².
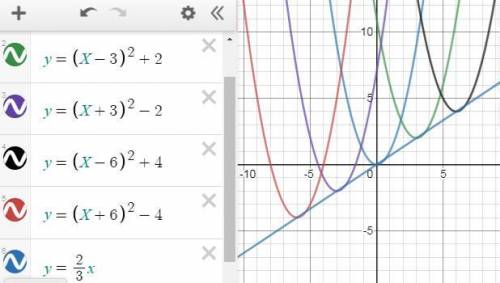
Прикрепляю их как фото. Если все графики построить на одной координатной плоскости, то можно увидеть, что они располагаются на одной прямой. Точки этой прямой
х: 0; 3; 6; -3; -6
у: 0; 2; 4; -2; -4
Эти точки соответствуют вершинам пяти взятых мной парабол.
Прямая - это график линейной функции y=kx. k - это коэффициент, который нужно найти. поставляем любую точку из таблицы выше (не (0;0)), например (3;2). х=3, у=2, получаем уравнение 2=k*3, k=2/3. график прямой линии и графики всех парабол прикреплен на втором фото. функция графика прямой y = 2/3 * x
Дело в том, что вместо а можно подставить абсолютно любое число. Хоть -100, хоть 0,2973, вообще любое. И какое бы число ни было, вершина параболы будет лежать на этой прямой
тогда (1-х1)(1-х2)...(1-хn)(1+f)=p - простому числу
это возможно если
(1-хi)=1- (a корней);
(1-хj)=-1-(b корней);
(1-хn)=p*(-1)^b - единственный корень
(1+f)=1;f=0;x=0
среди корней могут быть целые числа 0;2;1-p или 1+p
так как корень не единственный и корни натуральные (положительные), то остается 2-нечетное число корней и 1+p - один корень