Если мастер и ученик будут работать врозь, то мастер сможет побелить потолок за 3 часа, а ученик - за 7 часов.
Объяснение:
Задание
Мастер может побелить потолок в квартире на 4 часа быстрее чем его ученик. Если они будут работать вместе, то справятся с работой за 2,1 час. За какое время смогут побелить потолок мастер и ученик, если будут работать врозь?
Решение
1) Пусть х - время работы ученика, тогда (х-4) - время работы мастера.
2) Принимая весь объём работы равным 1,0, выразим производительность мастера и ученика:
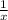 - производительность ученика, то есть объём работы, выполняемой учеником за 1 час;
- производительность ученика, то есть объём работы, выполняемой учеником за 1 час;
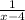 - производительность мастера, то есть объём работы, выполняемой мастером за 1 час.
- производительность мастера, то есть объём работы, выполняемой мастером за 1 час.
3) Согласно условию задачи, работая вместе, мастер и ученик за 2,1 часа выполнят весь объём работы, который мы приняли равным 1. Составим уравнение и найдём х:
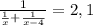
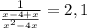
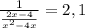
х² - 4х = 2,1 · (2х - 4)
х² - 4х - 4,2х + 8,4 = 0
х² - 8,2х + 8,4 = 0
Находим корни по формуле приведённого квадратного уравнения: х₁,₂ равно половине второго коэффициента, взятого с противоположным знаком, ± корень квадратный из квадрата этой половины без свободного члена:
х₁,₂ = 4,1 ± √ (4,1² - 8,4) = 4,1 ± √(16,81 - 8,4) = 4,1 ± √8,41 = 4,1 ± 2,9
х₁ = 4,1 + 2,9 = 7 часов - время работы ученика;
х₂ = 4,1 - 2,9 = 1,2 часа - данный корень отбрасываем, так как иначе получится, что время работы мастера будет величиной отрицательной.
Таким образом, если ученик будет работать один, то он выполнит всю работу за 7 часов, а мастер за:
7 - 4 = 3 часа.
ответ: если мастер и ученик будут работать врозь, то мастер сможет побелить потолок за 3 часа, а ученик - за 7 часов.
В решении.
Объяснение:
Решить систему неравенств:
х² - 2х - 48 >= 0
-7(x - 3) > -3x + 1
Решить первое неравенство:
х² - 2х - 48 >= 0
Приравнять к нулю и решить квадратное уравнение:
х² - 2х - 48 = 0
D=b²-4ac =4 + 192 = 196 √D=14
х₁=(-b-√D)/2a
х₁=(2-14)/2
х₁= -12/2
х₁= -6;
х₂=(-b+√D)/2a
х₂=(2+14)/2
х₂=16/2
х₂=8.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -6 и х= 8.
Решение первого неравенства: х∈(-∞; -6]∪[8; +∞).
Решить второе неравенство:
-7(x - 3) > -3x + 1
-7х + 21 > -3x + 1
-7x + 3x > 1 - 21
-4x > - 20
4x < 20 знак неравенства меняется при делении на минус
x < 5.
Решение второго неравенства: х∈(-∞; 5).
Отметить на числовой оси интервалы решений двух неравенств и найти пересечение решений (решения, которые подходят двум неравенствам).
-∞ -6 5 8 +∞
Решение первого неравенства: х∈(-∞; -6]∪[8; +∞). Штриховка от - бесконечности до х= -6 и от х= 8 до + бесконечности.
Решение второго неравенства: х∈(-∞; 5). Штриховка от - бесконечности до х= 5.
Пересечение решений (двойная штриховка) х∈(-∞; -6].
Обозначим скорость движения из А в В через х км/ч,время движения 3 ч,тогда путь =3х км.Из В в А скорость х+2,время 2(1/2)ч=5/2ч Путь найдем,как (х+2)*5/2.Но это одно и то самое расстояние.Тогда 3х=5/2(х+2), 6х=5х+10, х=10(км/ч)