1. Область значений функции у=cos x, так же, как и функции y=sin x равна [-1;1].
-1 ≤ cos 2x ≤ 1
-2 ≤ 2cos 2x ≤ 2
-3 ≤ 2cos 2x - sin x ≤ 3
-4 ≤ 2 cos 2x - sin x -1 ≤ 2
ответ. [-4;2]
2. Перепишем данное уравнение прямой в виде у=kx+b.
y=-√3/2 + 1
k₁=-√3/2
Находим коэффициент k₂, пользуясь формулой.
tg α = |(k₂-k₁) / (1+k₁k₂)|
tg 60°=√3
Находим, что k₂=√3/5=0,2√3
Подставляя значение k₂ и координаты данной точки в общее уравнение прямой, находим b.
0,2√3 · (-4) + b = -2
b = -2 + 0,8√3
Уравнение будет иметь вид у=0,2√3 х - 2 + 0,8√3
ищем определитель через разложение по 1-му столбцу:
2 1 -1
Δ₁₁= 2 -1 3
0 1 2
определитель для этого минора.
∆₁₁ = 2*((-1)*2-1*3)-2*(1*2-1*(-1))+0*(1*3-(-1)*(-1)) = -16
минор для (2,1):
-1 0 3
Δ₂₁= 2 -1 3
0 1 2
определитель для этого минора.
∆₂₁ = (-1)*((-1)*2-1*3)-2*(0*2-1*3)+0*(0*3-(-1)*3) = 11
минор для (3,1):
-1 0 3
∆₃₁ = 2 1 -1
0 1 2
определитель для этого минора.
∆3,1 = (-1)*(1*2-1*(-1))-2*(0*2-1*3)+0*(0*(-1)-1*3) = 3
минор для (4,1):
-1 0 3
Δ₄₁ = 2 1 -1
2 -1 3
определитель для этого минора.
∆₄₁ = (-1)*(1*3-(-1)*(-1))-2*(0*3-(-1)*3)+2*(0*(-1)-1*3) = -14
определитель матрицы
∆ = (-1)⁽¹⁺¹⁾ *1*(-16) + (-1)⁽²⁺¹⁾ *3*11 + (-1)⁽³⁺¹⁾ *1*3 + (-1)⁽⁴⁺¹⁾ *4*(-14) = 10
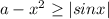
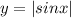 расположен выше оси ОХ.
расположен выше оси ОХ. 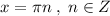 .
.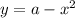 - это параболы , ветви
- это параболы , ветви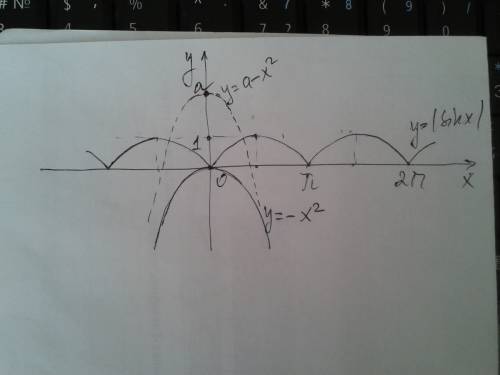
Скорректирую решение первой задачи.
Находим производную данной ф-ии:
Y' = -4sin2x + cosx >=0 (ищем промежутки возрастания(убывания) и крит. точки)
cosx(1 - 8sinx) >=0
Отмечаем на окружности четыре критические точки:
arcsin(1/8), П - arcsin(1/8), П/2, -П/2.
Анализируя получившиеся 4 интервала приходим к выводу, что в точках:
arcsin(1/8), П - arcsin(1/8) функция достигает своего максимума, а в точках:
П/2, -П/2 - минимума.
Найдем эти значения: (sinx = 1/8, cos2x = 1-2sin^2(x) = 31/32)
Уmax = 62/32 - 1/8 - 1 = 26/32 = 13/16
Ymin = -2 -1 -1 = -4
Получим следующую область значений: [ -4; 13/16]