Возводим обе части уравнения в квадрат и в куб. Получаем:
(х+1)³ = (3х-1)²
х³+3х²+3х+1=9х²-6х+1
х³-6х²+9х=0
х(х²-6х+9)=0
х₁=0 х²-6х+9=0
х₂=3
Сделав проверку, видим, что подходит только корень 3.
ответ. х=3
у=2(х-2)*-1
у=(2х-4)*-1
у=-2х+4
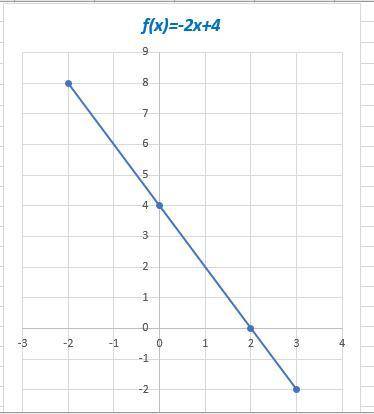
f(x)=-2x+4 - линейная функция, график - прямая
Область определения D(f) x∈R (множество всех действительных чисел)
Множество значений E(f) y∈R я
Нет максимума и минимума, непериодическая (непрерывна), ни четная, ни нечетная.
k=-2 => k<0 - функция убывающая, график образует тупой угол с положительным направлением оси 0Х.
График строится по 2-м точкам.
Можно найти точки пересечения графика с осями координат и построить график по ним.
Пересечение с осью 0Х: х=0 => y=-2*0+4=4 (0;4)
Пересечение с осью 0У: y=0 => х=-4/-2=2 (2;0)
у=2(х-2)*-1
у=(2х-4)*-1
у=-2х+4
f(x)=-2x+4 - линейная функция, график - прямая
Область определения D(f) x∈R (множество всех действительных чисел)
Множество значений E(f) y∈R я
Нет максимума и минимума, непериодическая (непрерывна), ни четная, ни нечетная.
k=-2 => k<0 - функция убывающая, график образует тупой угол с положительным направлением оси 0Х.
График строится по 2-м точкам.
Можно найти точки пересечения графика с осями координат и построить график по ним.
Пересечение с осью 0Х: х=0 => y=-2*0+4=4 (0;4)
Пересечение с осью 0У: y=0 => х=-4/-2=2 (2;0)

Пусть t = кор(3) (3х-1). Тогда х = (t^3 + 1)/3. Подставим в наше уравнение:
кор[((t^3 +1)/3) + 1] = t ОДЗ: t>=0 (х>=1/3)
кор((t^3 + 4)/3) = t
Возводим в квадрат:
t^3 + 4 = 3t^2 t^3 - 3t^2 + 4 = 0
Разложим на множители, представив в виде:
(t^3 - 4t^2 + 4t) + (t^2 - 4t + 4) = 0
t*(t-2)^2 + (t-2)^2 = 0
(t+1)*(t-2)^2 = 0
t1 = -1 не входит в ОДЗ
t2 = 2 тогда х = (8+1)/3 = 3
ответ: 3.