1. 7
2. 10
3. 3,8
4. 15,6
5. 13,0
Объяснение:
1. 450см / 70см ≈ 6,43. Если взять 6 дуг, то длина будет всего 420 см, а надо 450. Значит нужно взять минимум 7 дуг.
2. Потребуется (600 / 30) * 2 = 40 плиток на одну дорожку. На две потребуется 80 плиток. Они продаются в упаковках по 8шт., значит нужно взять минимум 10 упаковок.
3. Так как длина полуокружности = 6, то полная окружность равна 12, а она задаётся формулой C = 2πR, где R - тот радиус (высота теплицы). Искомая величина будет диаметром, то есть 2R. Решив уравнение "12 = 2πR", найдём, что R ≈ 1,9. Значит 2R = 3,8
4. Рассмотрев сторону основания, заметим, что её длина равна 3,8 (из пункта 3.), а дорожки занимают 0,6*2м (их две, они шириной по 0,6м). Значит на грядки остаётся 2,6м. Умножим на длину теплицы, получим 15,6м.
5. Требуемая величина будет равна половине площади окружности радиуса = высоте теплицы. Однако, таких стороны в теплице 2, значит искомая площадь = Sокр. = πR². Ранее вычислив R, подставим и посчитаем. S = 11,3354. Посчитав 15% от этого числа (15% = 1,70031) прибавим их к площади и получим искомую величину. = 13,03571. Округлив до десятых получим ответ 13,0
Расстояния:
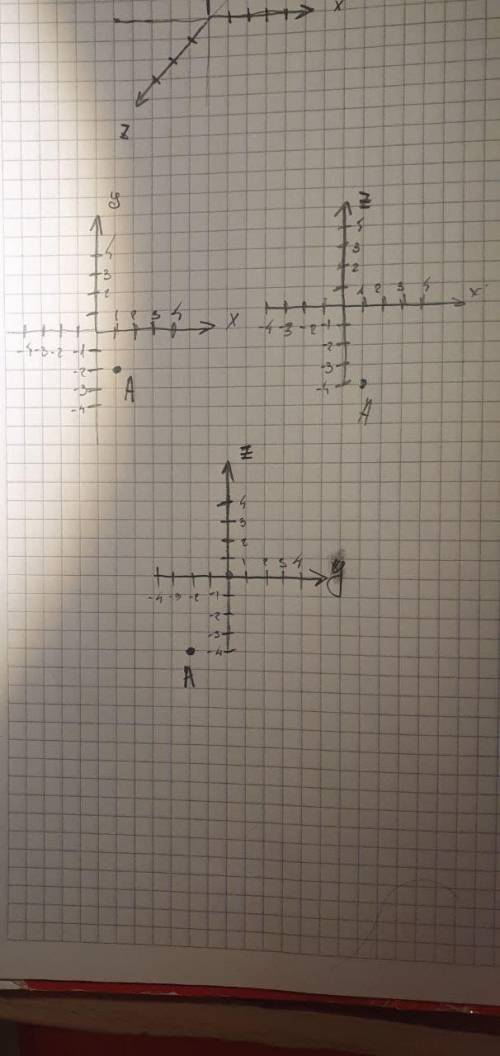
от точки A до координатной плоскости
1) xy = 4
2) xz = 2
3) yz = 1
Объяснение:
Для начала изображение. Очень сложно изобразить точку в трехмерном пространстве на бумаге, поэтому я нарисовал точку на 3-х плоскостях (xy, xz, yz)
Теперь найдем растояние точки от каждой плоскости. Пусть надо найти расстояние от точки A до плоскости xy. То есть x и y у нас те же а z=0.
Что это значит?
Вспомним формулу расстояния точки А(x1, y1, z1) до точки B (x2, y2, z2)
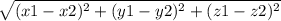
в нашем примере получается что x1 = x2 и y1 = y2. А что получается когда у нас 2 числа при отнимании равны? 0! А z2 у нас 0. Как я объяснял еще раньше.
поэтому функция иммет вид
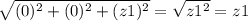
Чтобы найти корни многочлена, надо приравнять его к нулю и решить уравнение. Для квадратного уравнения вида ax²+bx+c=0 верно следующее:
Если D<0, то корней нет;
Если D=0, то корень один;
Если D>0, то корней два;
Где D - дискриминант, равный b²-4ac.
а)
3x²-8x+2=0; 3x²+(-8)·x+2=0
D = (-8)²-4·3·2 = 64-24 = 40 > 0.
ответ: 2 корня.
б)
ответ: 1 корень.
в)
m²+(-3)·m+3=0
D = (-3)²-4·1·3 = 9-12 = -3 < 0
ответ: 0 корней.