Объяснение:
a)
x²=xy+3
xy=-2 подставим это в первое уравнение
x²=-2+3=1
x₁=1 y₁=-2/x=-2
x₂=-1 y₂=-2/(-1)=2
b)
x(y+1)=0
x+5xy+y=4
1й случай х=0 подставим во второе уравнение получим у=4
2й случай у+1=0 у=-1 подставим во второе уравнение получим
х-5х-1=4 ; -4x=5 x=-5/4=0,8
c) этот пример не видно
другой номер
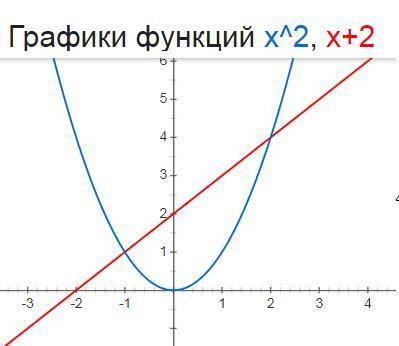
a) y=x^2 это парабола с вершиной в точке (0;0)
y=x+2 это прямая у=х которая является биссектрисой первой координатной четверти перемещенная вверх на 2 единицы
построим схематично графики
видно что графики имеют две точки пересечения значит система имеет два решения
если решать этот пример через дискриминант то тогда
x²=x+2
x²-x-2=0
d=1+8=9
x₁₋₂=(1±3)/2={-1;2}
Объяснение:
Задание 2.
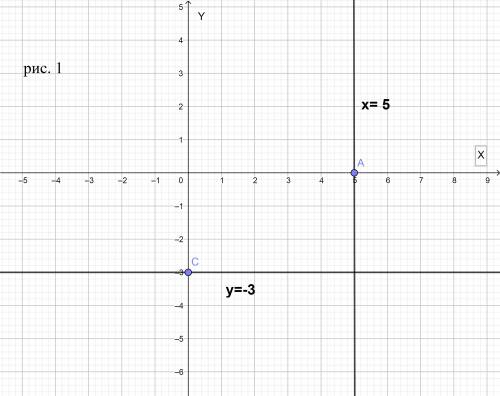
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
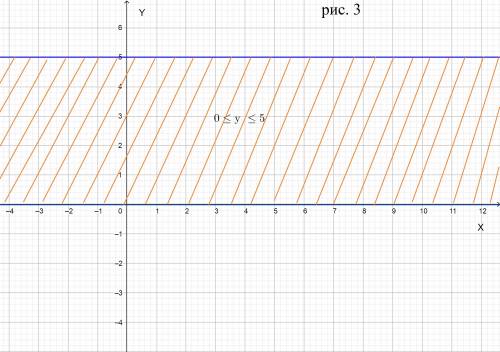
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
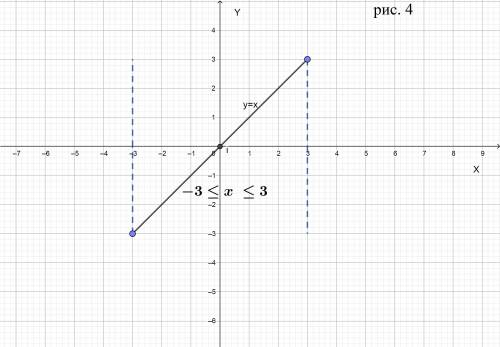
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
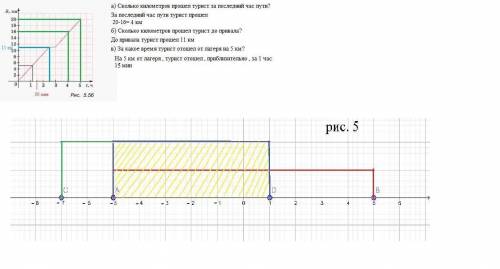
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]

х² +рх + q = 0
х₁+х₂=-р
х₁·х₂=q
Поэтому
1) х₁+х₂=-3+5=2 ⇒ р =- 2
х₁·х₂=(-3)·5=-15 ⇒ q = -15
Уравнение
х² - 2х -15 = 0
2)х₁+х₂=3а+1+5а-2==8а-1 ⇒ р=8а-1
х₁·х₂=(3а+1)(5а-2)=15а²+5а-6а-2=15а²-а-2
Уравнение
х² +(8а-1)х +(15а²-а-2) = 0