Действительных корней нет.
Комплексные корни:
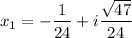
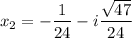
Объяснение:
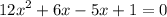
Приводим подобные слагаемые:
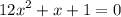
Это обычное квадратное уравнение. Решим через дискриминант.
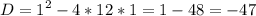
Дискриминант меньше нуля, следовательно действительных корней нет.
Найдем комплексные корни.
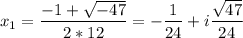
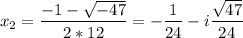
Теория:
Стандартный вид квадратного уравнения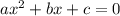 
, 
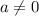
Дискриминант 
Если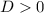 
, то квадратное уравнение имеет два действительных корня.
Если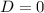 
, то квадратное уравнение имеет один действительных корень.
Если 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида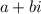 
, где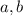 
- действительные числа, 
- мнимая единица.
Мнимая единица - число, для которого выполняется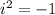 
ответ: потому что уравнение x²-5*x+36 не имеет действительных корней.
Объяснение:
Если уравнение a*x²+b*x+c=0 имеет действительные корни x1 и x2, то a*x²+b*x+c=a*(x-x1)*(x-x2), то есть в этом случае квадратный трёхчлен a*x²+b*x+c можно представить в виде произведения двух многочленов первой степени x-x1 и x-x2. В нашем же случае уравнение x²-5*x+36=0 имеет отрицательный дискриминант D=(-5)²-4*1*36=-119, поэтому это уравнение не имеет действительных корней. А значит, данный квадратный трёхчлен нельзя представить в виде произведения многочленов первой степени.
2)А вот с другими дробями будет несколько сложнее, придётся с ними повозиться.
Итак, нам нужно представить 0,(3) в виде обыкновенной дроби. Как я уже сказал, сделать это не совсем просто. Для перевода будет использоваться формула, которую я сейчас напишу во вложениях. Затем мы должны будем просчитать компоненты этой формулы )
Формулу наверное посмотрели уже ) Сейчас мы будем по очереди считать все эти буковки, чтобы потом подставить их.
Начнём с того, что Y - это целая часть нашей дроби периодической. У нас она равна 0.
Вычислим k. Что такое k? k - это число цифр в периоде. У нас одна цифра в периоде(3), поэтому k = 1.
Вычисляем теперь m - это число цифр в дробной части, не входящих в период. Видим, что в дробной части у нас только период, поэтому m = 0.
Вычисляем a. Это ни что иное, как натуральное число, образованное всеми цифрами дробной части. Иначе говоря, берём все цифры в дробной части(из периода тоже берём), записываем их как они написаны, это и есть а. В нашем случае а = 3. А b - это число, образованное цифрами дробной части, не входящими в период!
b = 0 - это вполне очевидно.
Теперь записываем формулу, считаем и получаем искомую обыкновенную дробь:
X = 0 + (3-0)/9 = 3/9 = 1/3 - это и есть ответ.
Проверить легко: разделим числитель на знаменатель, получим 0.3333333333..., то есть 0,(3)
Аналогично сама сделать. ответ проверь делением.