2(1-cos²x)-3cosx-1=0
2-2cos²x-3cosx-1=0
2cos²x+3cosx-1=0
Вводим замену cosx=t
2t²+3t-1=0
D=9+8=17
t=(-3±√17)/4
cosx=(-3+√17)/4 cosx≠(-3-√17)/4 - корней нет
x=±arccos((-3+√17)/4) + 2πn, n∈Z
ответ. x=±arccos((-3+√17)/4) + 2πn, n∈Z
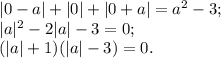
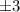
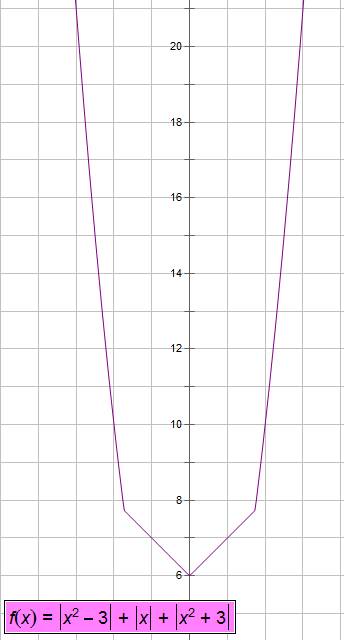
5% = 0,05; 4% = 0,04
Пусть вкладчик внёс на первый счёт х грн, тогда доход по этому счёту составил 0,05х грн.
Пусть вкладчик внёс на второй счёт у грн, тогда доход по этому счёту составил 0,04у грн.
Если средства, внесённые на разные счета, поменять местами, то годовой доход по двум вкладам составит
0,04x + 0,05y = A гривен.
Составим систему
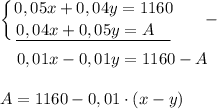
1) Если средства, внесённые на два счёта были одинаковы, то годовой доход не изменится :
x = y, x - y = 0, A = 1160
2) Если на первый счёт было внесено больше денег, чем на второй счёт, то годовой доход уменьшится :
x > y, x - y > 0, A < 1160
3) Если на первый счёт было внесено меньше денег, чем на второй счёт, то годовой доход увеличится :
x < y, x - y < 0, A > 1160
ответ : изменение годового дохода будет зависеть от количества внесённых денежных средств на разные счета.
2(1 - cos^2 x) - 3cosx - 1 = 0
2cos^2 x + 3cosx - 1 = 0 D = 17
cosx = (-3+кор17)/4
х = +- arccos((-3+кор17)/4) + 2Пk, k прин. Z.