Question

Две бригады из которых вторая начинает работать на 5 дней позже первой, закончили работу за 15 дней, считая от начала работы второй бригады. если бы эта работа была поручена каждой бригаде отдельно, то для её выполнения первой бригаде понадобилось бы на 10 дней больше , чем второй.за сколько дней может выполнить эту работу каждая бригада, работая отдельно?

Answer 1

Пусть второй бригаде понадобилось бы х дней на то, чтобы в одиночку сделать эту работу.

Тогда первой бригаде понадобилось бы x+10 дней.

Часть работы, которую за день выполняет вторая бригада в одиночку, выражается числом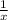 $\frac{1}{x}$.

Тогда часть работы, выполняемую в день первой, выразим так: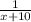 $\frac{1}{x+10}$.

Сначала, по условию, первая бригада работала 5 дней в одиночку, так что она успела сделать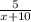 $\frac{5}{x+10}$ всей работы.

Потом к ней подключилась вторая, и в течение 15 дней они выполнили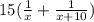 $15(\frac{1}{x}+\frac{1}{x+10})$ всей работы.

Вся выполненная работа выражается следующим образом:

$\frac{5}{x+10}+\frac{15}{x}+\frac{15}{x+10}=1$

Далее, $\frac{20}{x+10}+\frac{15}{x}-1=0$

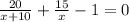
Избавимся от знаменателя дроби и приведем подобные члены, тогда получим:

$-x^2+25x+150=0$

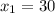Получим $x_1=30$, $x_2=-5$. Через x мы выражали количество дней, которое потребовалось бы второй бригаде на то, чтобы справиться в одиночку, а оно не может быть отрицательным. Значит, вторая бригада сделала бы эту работу за 30 дней, а первая - за 40.