1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
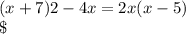
Переобразуем:
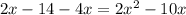
Переносим в общую сторону (левую) и меняем знаки:
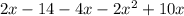
Сокрашаем:
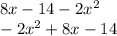
ответ: 
Старший коэффициент: 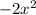
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А) 
В) 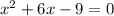
С) 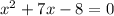
D) 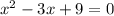
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
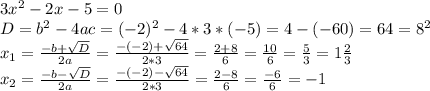
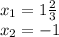
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
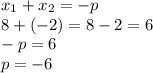


ответ: 
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят  и
и 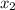 совпадают.
совпадают.
Если p = 0, то 

ответ: c = 32
3. б) Найдите эти корни уравнения
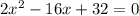
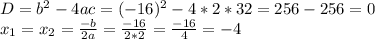
ответ: 
(-∞;3) ∪ (
Объяснение:
Найдите промежутки возрастания и убывания функции, точки экстремума
1) Функция определена на всей области R. Значит она является непрерывной на всей области определения
2) Найдем производную данной функции
Для того, чтобы найти точки экстремума данной функции нужно найти в каких точках производная равна нулю
разделим на 3
Значит точки экстремума х=1 и х=-3
3) Чтобы определить какая из данных точек является точкой максимума, а какая точкой минимума необходимо рассмотреть значение производной на полученных интервалах
___+-+
-3 1
Если производная на промежутке принимает положительное значение то функция на данном промежутке возрастает, если отрицательное- то функция убывает
Значит на промежутке (-∞;3) ∪ (
Ход урока:
1. Организационный момент.
2. Актуализация знаний.
1) На доске записать числа, которые учащиеся должны представить, как степень некоторого простого числа:
2) Вспомнить свойства степени по примерам:
а) б)
3) Рассмотреть решение примера № 1190.
3. Объяснение нового материала.
Данную тему можно предложить учащимся разобрать самостоятельно (алгоритм работы с книгой предлагается ранее). Провести обсуждение нового материала. Учитель должен рассказать о применении стандартного вида числа (остановиться на физических задачах). Рассмотреть приведение к стандартному виду числа на примерах:
(порядок числа равен 3);
(порядок числа равен – 2)
4. Закрепление нового материала.
Разобрать решение примеров № 1197, 1198, 1200, 1203(а, г), 1204, 1205(а, г), 1207, 1209.
Для сильных учеников предлагается решить задания № 1210, 1212.
5. Самостоятельная работа.Вариант 1Вариант 21) Решить уравнения:а)
б) а)
б) 2) Упростить, если возможно вычислить выражения:а) б) а) б) 3) Сравнить значения:а) и
б) и 0,004.а) и
б) и 0,0027.ответы:Задание1 (а)1 (б)2 (а)2 (б)3 (а)3 (б)I9,7; 1,3большеменьшеII5,8; 8,21меньшебольше