(1;3)
Объяснение:
1) Метод алгебраического сложения
{х+у=4 умножаем на (-2)
2х-у=5
{-2х-2у=-8
2х-у=5
Складываем уравнения
-3у=-3 умножаем на (-1)
у=3/3
у=1
Подставляем значение в одно из уравнений
х+у=4
х+1=4
х=4-1
х=3
ответ: (1;3)
2) Метод Подстановки
{х+у=4
2х-у=5
{х=4-у
2х-у=5
Подставляем значение х первого уравнения, во второе
2х-у=8
2(4-у)-у=5
8-2у-у=5
8-3у=5
-3у=5-8
-3у=-3
у=3/3
у=1
Подставляем значение у в первое уравнение
х=4-у
х=4-1
х=3
ответ: (1;3)
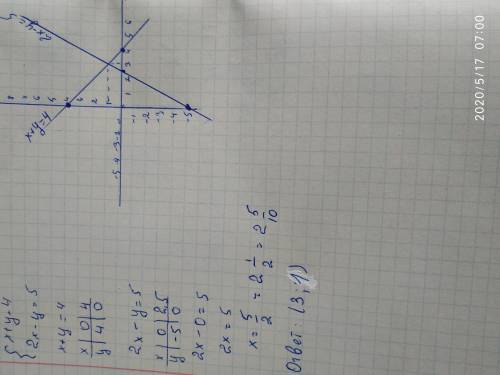
3) Графический
{х+у=4
2х-у=5
Берём первое уравнение
х+у=4
Пусть х будет 0, тогда у будет равно
0+у=4
у=4
Первая координата нашей прямой (0;4)
Пусть у будет 0, тогда х будет...
х+0=4
х=4
Вторая координата нашей прямой
(4;0)
Строим прямую в прямоугольной координатной плоскости, с координатами
(0;4) (4;0)
Берём второе уравнение
2х-у=5
Пусть х будет 0, тогда у будет равно
2*0-у=5
-у=5
у=-5
Первая координата нашей прямой (0;-5)
Пусть у будет равно 0, тогда х будет...
2х-0=5
2х=5
х=5/2
х=2целых1/2
х=2,5
Вторая координата прямой (2,5;0)
Строим прямую, в прямоугольной координатной плоскости, с координатами (0;-5) (2,5;0)
Точкой пересечения двух прямых, будет решением для данной системы уравнений
Координаты пересечения двух прямых является (1;3)
ответ: (1;3)
Для начала вспомним т. Виетта
для уравнения вида x²+px+q=0
выпоняется : x₁+x₂= -p; x₁*x₂=q
теперь решение:
1) x²-13x+q=0
x₁=12.5
x₁+x₂= -(-13)=13
12.5+x₂=13
x₂=0.5
x₁*x₂=12.5*0.5=6.25= q
тогда уравнение будет x²-13x+6.25=0
2) 10x²-33x+c=0
приведем его к стандартному виду
x²-(33/10)x+(c/10)=0
x²-3.3x+(c/10)=0
x₁=5.3 тогда 5.3+x₂=3.3; отсюда x₂= -2
c/10=5.3*(-2)=-10.6; Значит с= -106
Уравнение будет иметь вид 10x²-33x-106=0
3) x²+2x+q=0
x₁²-x₂²=12
(x₁-x₂)(x₁+x₂)=12
(x₁-x₂)*(-2)=12
x₁-x₂= -6
x₁=x₂-6
Теперь найдем корни
x₁+x₂=x₂-6+x₂=-2
2x₂=4
x₂=2; x₁= -4
тогда q=2*(-4)= -8
Уравнение примет вид x²+2x-8=0
его корни x₁²-x₂²=(-4)²-(2)²=16-4= 12