Question

F(x)= 1/ квадратный корень из 2х- х2 (в квадрате) найти область определения функции

Answer 1

На ноль делить нельзя; подкоренное выражение должно быть неотрицательным.

Для функции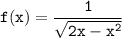 $\tt \displaystyle f(x)=\frac1{\sqrt{2x-x^2 }}$ :

$\displaystyle \begin{Bmatrix}\sqrt{2x-x^2 } \ne 0\\ 2x-x^2 \ge 0\end{matrix} \quad \begin{Bmatrix}2x-x^2\ne 0\\ 2x-x^2 \ge 0\end{matrix} \\ \\ 2x-x^20\; \;\; \begin{vmatrix} \\\end{matrix} \cdot ($-$1)<0\\ \\ x^2-2x<0\\ x(x-2)<0$

Решим методом интервалов.

x∈(0;2)

ответ: D(f) = (0;2).

Для функции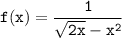 $\tt \displaystyle f(x)=\frac1{\sqrt{2x} -x^2 }}$ :

$\displaystyle \begin{Bmatrix}\sqrt{2x} -x^2 \ne 0\\ 2x\ge 0\qquad \end{matrix} \quad \begin{Bmatrix}\sqrt{2x} \ne x^2 \\ x\ge 0\quad \end{matrix} \\ \\ \begin{Bmatrix}2x\ne x^4 \ge 0\\ x\ge 0\qquad \end{matrix} \quad \begin{Bmatrix}x(x^3 -2)\ne 0\\ x\ge 0\qquad \end{matrix} \\ \\ \begin{Bmatrix}x\ne \{ 0;\sqrt[3]2\} \\ x\ge 0\qquad \end{matrix}$

$\displaystyle x\in (0;\sqrt[3]2)\cup (\sqrt[3]2 ;+\infty )$

ответ: $\tt \displaystyle D(f)=(0;\sqrt[3]2)\cup (\sqrt[3]2 ;+\infty ).$