(a - 7)² - 2(a - 7) (a + 7) + (a + 3)² = a² - 14a + 49 - 2(a² - 49) + a² + 6a + 9 = a² - 14a + 49 - 2a² + 98 + a² + 6a + 9 = -8a + 156 = 156 - 8a
156 - 8a = 156 - 8*(1/4) = 156 - 2 = 154
Уравнение не имеет корней не только при к=10.
(z-8)z=k(k-10)
z^2-8z-k^2-10k=0
D=64-4(-k^2+10k)=4k^2-40k+64
Если дискриминант меньше 0, то данное уравнение не имеет корней, поэтому переходим к решению неравенства:
4k^2-40k+64<0
k^2-10k+16=0
D=100-4*16=36
k1=(10-6)/2=2
k2=(10+6)/2=8
Двумя точками числовая ось разбивается на три интервала. Методом интервалов определяем, что данное уравнение не имеет решений тогда, когда К принадлежит интервалу (2;8).
Значит все натуральные значения К, при которых уравнение не имеет корней:
3; 4; 5; 6; 7 и 10 (так как при 10 обращается в ноль знаменатель первой дроби из условия).
Сумма всех этих натуральных чисел равна 35.
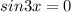
3x - неизвестная и она будет равна значению угла в точке 0
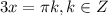
а чтобы найти x, нужно обе части поделить на 3
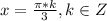
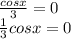
представляем это как 1/3. обе части делим на 1/3. 0 делить на 1/3 так и будет ноль.
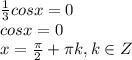
cosx=-1
впринципе табличное значение. но вообще хорошо бы представлять себе тригонометрический круг. косинус на оси x. отмеряем -1 на оси x. чтобы спроецировать -1 на ось икс, на нужно пройти 180 градусов по часовой стрелке или π, в радианах. добавим сюда ещё период косинуса 2π*k
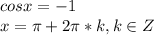
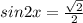
опять же делаем как первом примере
2x приравниваем к значению угла в √2/2
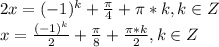
Но это все - таличные значения, их нужно просто выучить.
(a-7)²-2(a-7)(a+7)+(a+3)²=а²-14а+49-2(a²-49)+ a²+6a+9=а²-14а+49-2а²+98+а²+6а+9=
= -8а+156=156-8а при а=1/4=0,25,имеем
156-8*1/4=156-2=154