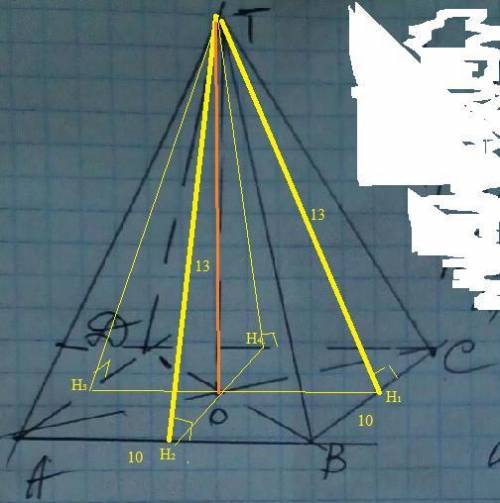
Расстояние от точки до сторон квадрата равно 13 см. Найдите расстояние от точки до плоскости квадрата, если сторона квадрата равна 10 см. можете объяснить, с рисунком
Объяснение:
Расстояние от точки Т до плоскости отрезок ТО ⊥ ( АВС) . Значит ТО перпендикулярен любой прямой лежащей в плоскости.
Т.к. расстояние -это перпендикуляр, то опустим перпендикуляры из точки Т на стороны квадрата : ТН₁ , ТН₂ , ТН₃ , ТН₄. Тогда прямоугольные треугольники ( на рисунке желтые) равны по катету и гипотенузе ( апофема боковой грани).⇒точка О -центр вписанной окружности и еще т. пересечения диагоналей квадрата.
Н₁ Н₃= 10 , ОН₁=5 , из ΔТОН₁ , по т. Пифагора ТО=√(13³-5²)=√144=12 (см)
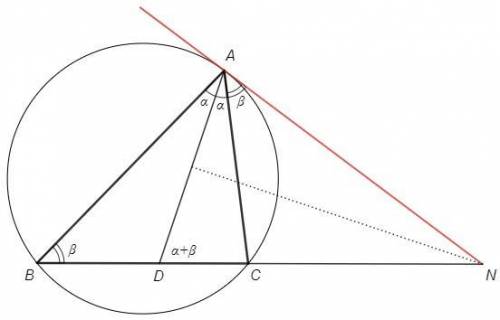
Точка N лежит на серединном перпендикуляре к AD, следовательно равноудалена от концов отрезка.
△AND - равнобедренный, DAN=ADN
DAN =A/2 +NAC
ADN =A/2 +B (внешний угол △BAD)
=> NAC =B =∪AC/2
Угол между прямой NA и хордой AC равен половине дуги, стягиваемой хордой, следовательно NA является касательной.
Докажем этот признак для острого угла NAC.
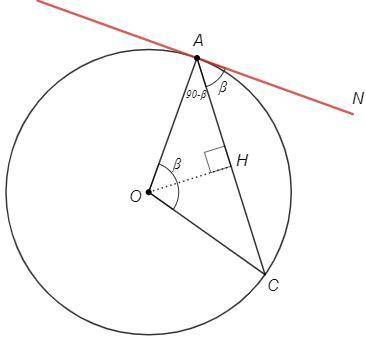
NAC =∪AC/2 =AOC/2 =AOH
△AOC - равнобедренный, OH - биссектриса и высота
OAH =90-AOH =90-NAC => OAN =OAH+NAC =90
Прямая NA перпендикулярна радиусу OA, следовательно является касательной.
Для тупого угла как для смежного с NAC:
180-NAC =(360-∪AC)/2 => NAC=∪AC/2, далее по доказанному.
х+2х+х+2х=24
Теперь решим его:
6х=24
х=24/6
х=4 - меньшая сторона прямоугольника.
Тогда вторая сторона будет равна 2*4=8.
Площадь будет равна 8*4=32см^2.