для начала находим корни данного в условии уравнения x^2-3x+1=0
D=9-4=13
x1=[3+кореньиз(13)]/2
x2=[3-кореньиз(13)]/2
Составьте уравнение корни которого на 1 больше корней уравнени:
Наши новые корни X=x1+1 и X=x2+1 получаем X=[5+кореньиз(13)]/2
X=[5-кореньиз(13)]/2
Воспользуемся теоремой Виета ,которая говорит нам: x^2+px+q=0
x1+x2=-p
x1*x2=q
Подставим в эту теорему наши новые корни (которые на 1 больше старых ):
[5+кореньиз(13)]/2+[5-кореньиз(13)]/2=-p
[5+кореньиз(13)]/2*[5-кореньиз(13)]/2=q
Таким образом наше квадратное уравнение (которое просят составить в условии) примет вид : x^2-5x+[(25-13)]/2=0-->> конечный вид x^2-5x+6=0
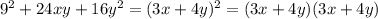
возможно 5 случая:
1) допустим, х-отрицательное, а y положительноетогда сумма (3x+4y) будет отрицательной, а произведение (3x+4y)(3x+4y) будет положительно.(тоже самое будет, если наоборот y-отрицательное, а x положительное)
2) допустим, х и y отрицательные,тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) тоже будет положительно.
3) допустим, х и y положительные, тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) соответственно будет положительно
4) допустим любая из переменных x или y=0, тогда независимо от неравной нулю переменной произведение (3x+4y)(3x+4y) будет положительно
и 5) самый простой случай, когда и х и y =0, тогда и сумма и произведение будут равны нулю, т.е. неотрицательны.
во всех 4х случаях выходит, что выражение неотрицательно, ч.т.д.
Строим у=-х²,сдвигаем ось ох на 9 единичный отрезков вниз и ось оу на 2 единичный отрезка влево.Вершина в точке (2;9)-точка максимума,точки пересечения с осями (0;5),(-1;0),(5;0)
а) значение у,при x=4, у=5 x=-0,5; у≈3
б) значение х, при y=2; х≈-0,7 х≈4,7
в) нули функции; (0;5),(-1;0),(5;0)
г) промежутки в которых у > 0 (-1;5) и в которых у <0; (-∞;-1) и (5;∞)
д) промежуток,в котором функция возрастает, (-∞;2) убывает; (2;∞)
е) область определения (-∞;∞) и область значений функции. (-∞;9]
2)y=-2x²+4x+3=-2(x-1)²+5
Вершина (1;5)-точка максимума
Наибольшее у=5