Задание 1.
Треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны.
Иначе, для сторон a; b; c должны выполняться следующие три неравенства:
a+b>c; a+c>b; b+c>a
а) стороны равны a=10 см; b=15 см; c=25 см;
10+15=25
10+25>15
15+25>25
Три неравенства не выполняются, значит, треугольник не существует.
б) стороны относятся как 3:5:10;
a=3x; b=5x; c=10x;
3x+5x<10x;
3x+10x>5x
5x+10x>3x
Три неравенства не выполняются, значит, треугольник не существует.
Если сумма углов треугольника не равна 180 градусам, то треугольник не существует.
в) углы равны 46°, 64° и 80°;
46°+64°+80° = 190°
190°≠ 180° треугольник не существует.
г) углы относятся как 3:5:10.
3х+5х+10х=180°
18х = 180°
х = 180° : 18
х = 10°
3·10°=30°
5·10°=50°
10·10°=100°
30°+50°+100°=180°
Треугольник с углами 30°; 50°; 100° треугольник существует.
Задание 2.
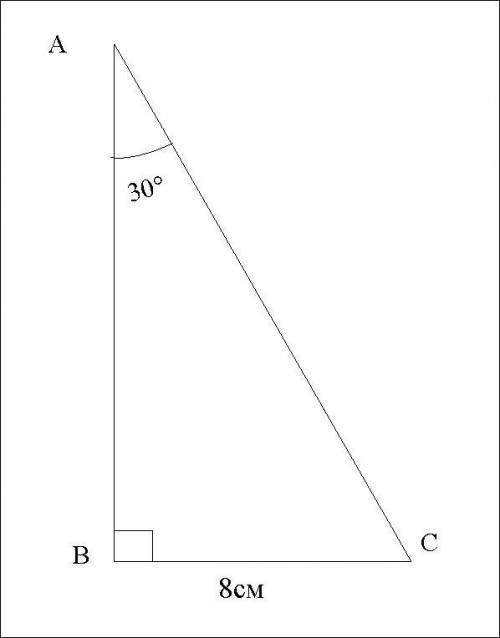
Перпендикуляр AB, наклонная AC и прямая ВС образовали прямоугольный ΔАВС.
∠А=30°;
ВС=8см.
Найти АС.
Решение
В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы.
У нас катет ВС лежит против угла величиной 30°, значит,
ВС = 1/2 АС.
А гипотенуза АС будет в 2 раза больше катета ВС.
АС = 2ВС
АС=2·8см
АС=16см
у=8-2х у-х=3 2х=-3
х-(8-2х)=4 у-(1+2у)=3 -3у-3у=4
х=4 у=-4 у=\frac{-2}{3}
у=8-2*4 х=1+2*(-4) 2х=-3х(-\frac{-2}{3})
у=0 х=-7 х=1
ответ: (4,0) ответ: (-7,-4) ответ: (1, -\frac{-2}{3})
Объяснение:
\frac{-2}{3} дробь я тут не разобрался в этом школьное знание и смог понять как делать дробь.
Если то нажми