24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
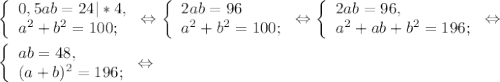

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
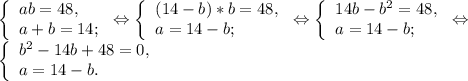
Решим квадратное уравнение:
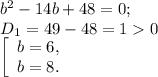
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
В решении.
Объяснение:
Задание на разность квадратов:
а² - в² = (а - в)*(а + в).
1) При каких значениях переменной x выражение (x-3)²-14² равно 0? Если таких значений несколько.
(x-3)²-14²=0
(х - 3 - 14)*(х - 3 + 14) = 0
(х - 17)*(х + 11) = 0
х - 17 = 0
х₁ = 17;
х + 11 = 0
х₂ = -11.
При х = 17 и х = -11 данное выражение равно нулю.
2) При каких значениях переменной x выражение ( x-9)²-8² равно 0? Если таких значений несколько.
( x-9)²-8²=0
(х - 9 - 8)*(х - 9 + 8) = 0
(х - 17)*(х - 1) = 0
х - 17 = 0
х₁ = 17;
х - 1 = 0
х₂ = 1.
При х = 17 и х = 1 данное выражение равно нулю.
3) При каких значениях переменной x выражение ( x-7)²-3² равно 0? Если таких значений несколько.
( x-7)²-3²=0
(х - 7 - 3)*(х - 7 + 3) = 0
(х - 10)*(х - 4) = 0
х - 10 = 0
х₁ = 10;
х - 4 = 0
х₂ = 4.
При х = 10 и х = 4 данное выражение равно нулю.
4) При каких значениях переменной x выражение ( x-9)²-17² равно 0? Если таких значений несколько.
( x-9)²-17²=0
(х - 9 - 17)*(х - 9 + 17) = 0
(х - 26)*(х + 8) = 0
х - 26 = 0
х₁ = 26;
х + 8 = 0
х₂ = -8.
При х = 26 и х = -8 данное выражение равно нулю.