ответ: y=x² - 6x +5
а=1, b= -6, c=5
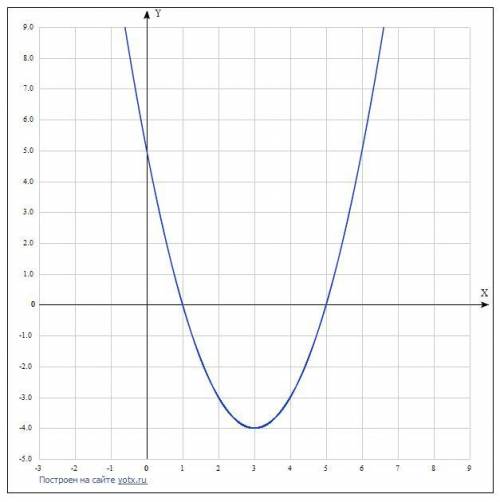
Это график параболы, ветви направлены вверх ( а>0)
1) надо найти координаты пересечения с осью ОХ
для этого найдём корни уравнения:
y=x²- 6x +5. По теореме Виета х₁=1, x₂=5
Координаты (1;0) и (5;0)
2) надо найти координаты пересечения с осью ОУ:
х=0
у=0²-6*0+5=5
координаты пересечения с осью ОУ: (0;5)
3) Найдём координаты вершины параболы
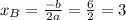
yв=3²-6*3+5=9-18+5=-4
координаты вершины параболы : (3;-4)
Можно построить таблицу точек
х 2 4 6
у -3 -3 5
Логарифмическая — функция, обратная потенциированию.
Построив график обратной функции и зеркально отразив его относительно прямой y = x, получим нужный нам график.
Итак, обратная к y=log2(x-2)
функция — это
x=2y+2
Строим график y=2x+2
Его можно получить из графика y=2x
смещением вверх на 2 (либо смещением оси y вниз на 2).
Это — быстровозрастающая функция, равная 1 при x = 0, стремящаяся к 0 на минус бесконечности. Располагается только в верхней полуплоскости (область значений y ≥ 0). Несколько точек для построения: x = 1, y = 2; x = 2, y = 4; x = 4, y = 16; x = -1, y = 0.5; x = -2, y = 0.25.
Отражением относительно прямой y = x получаем искомый график. y=2x +2
и заданной y=log2(x-2)
2^3x2^2x / 2^7 = 4
2 ^ 5x / 2^7 = 2^2
2 ^5x = 2 ^9
5X = 9
X = 1,8