Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
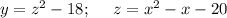
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
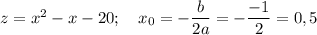 - координата вершины
- координата вершины
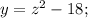 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
sinx * siny = 1/4
cosx * cosy = 3/4
Сложим и вычтем уравнения системы. Получаем
cosx * cosy + sinx * siny = 1
cosx * cosy - sinx * siny = 1/2
cos (x - y) = 1
cos (x + y) = 1/2
x - y = 2 * π * n
x + y = ±π/3 + 2 * π * m
Сложим и вычтем уравнения полученной системы
2 * х = 2 * π * n ± π/3 + 2 * π * m
2 * y = ± π/3 + 2 * π * m - 2 * π * n
x = π * n ± π/6 + π * m
y = ± π/6 + π * m - π * n
или
sinx*siny=1/4
cosx*cosy=3/4
Сложим и вычтем уравнения системы и по формулам косинуса суммы и разности перейдем к более простой системе:
cos(x+y) = 1/2, x+y = +-pi/3 + 2pik
cos(x-y) = 1, x-y = 2pik, вычтем из первого-второе:
Объяснение:
это как я понимаю
-2x+(-x)+2x+3x = -2x-x+2x+3x = -x+3x = 2x
x+(-2x)+3x = x-2x+3x = 2x
-x+(-x)+(-2x)+2x = -x-x-2x+2x = -x-x = -2x
-x-2x+3x = 0
2x+x+(-2x)-3x = 2x+x-2x-3x = x-3x = -2x