ответ: 30°
Объяснение:
1. Проведём из точки S высоту пирамиды SO. Точка O -- это центр ΔABC, лежит на пересечении медиан (так как ABCS -- правильная)
2. SB -- наклонная, SO ⊥ (ABC) ⇒ BO -- проекция SB на (ABC)
3. Так как BO -- проекция SB на (ABC), ∠(SB, (ABC)) = ∠(SB, BO) = ∠SBO -- искомый (по определению угла между прямой и плоскостью)
4. Рассмотрим ΔABC.
BB₁ -- медиана ⇒ СB₁ = 1/2 AC = 9/2
Так как ΔABC -- равносторонний, то
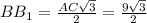
(можно найти и по теореме Пифагора из ΔBB₁C, т.к. BB₁ - высота)
Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2 : 1, считая от вершины. Тогда
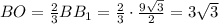
5. Рассмотрим ΔBSO:
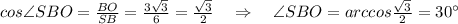

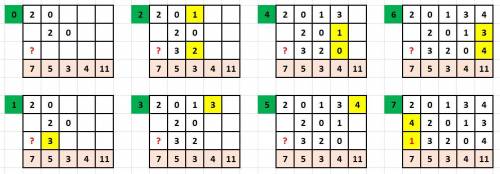
1. Во втором столбце осталась одна свободная клетка. Туда записывается 5-0-2=3.
2. В третьем столбце сумма двух свободных клеток должна равняться 3-0=3. Так как 0 в этом столбце уже есть, то эта сумма будет складываться из 1 и 2. 2 в первой строке уже есть, поэтому туда записывается 1, а в третью строку записывается 2.
3. В четвертом столбце получить четверку можно лишь сложив числа 0, 1 и 3. В первой строке уже есть цифры 0 и 1, значит туда записывается 3.
4. Оставшиеся два места в четвертом столбце должны занять цифры 0 и 1, но 0 уже есть во второй строке, значит туда записывается 1, а 0 записывается в третью строку.
5. В первой строке не хватает числа 4.
6. В последнем столбце сумма свободных клеток должна быть 11-4=7. Эту сумму можно получить только сложив 3 и 4, причем число 3 уже есть в третье строке. значит, его записываем во вторую строку, а в третью строку записываем 4.
7. Во второе строке не хватает числа 4, а в третьей - искомого числа - числа 1.
ответ: 1