Question

№1.значение какого извыражений является иррациональным? 1)\sqrt{18}*\sqrt{2} 2)(\sqrt{12}-\sqrt{23})*(\sqrt{12}+\sqrt{23}) 3)\frac{12}{27} 4)\sqrt{20} +2\sqrt{5} №2. решите уравнение. \frac{x-9}{x-6}=\frac{3}{4} №3. в прогрессии (b_{n}) b_{2}= -0,2, b_{5}=-25 найдите знаменатель прогрессии. №4. найдите значение выражиения (\frac{u}{v}+\frac{v}{u}+2)*\frac{uv}{v+u} при v=3\sqrt{2}+1, u= 4-3\sqrt{2}

Answer 1

1)\sqrt{18}*\sqrt{2} = √18 * √2 = √(9 * 3) * √2 = 3√2 * √2 = 3 * 2 = 6  - не является иррациональным

2) (\sqrt{12}-\sqrt{23})*(\sqrt{12}+\sqrt{23}) = (√12 - √23)(√12 + √23) = √12² - √23² = 12 - 23 = -11 - не является иррациональным

3)\frac{12}{27} =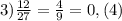 $3)\frac{12}{27} =\frac{4}{9}= 0,(4)$ - является иррациональным

4)\sqrt{20} +2\sqrt{5} =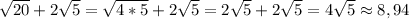 $\sqrt{20} +2\sqrt{5}=\sqrt{4*5} +2\sqrt{5} = 2\sqrt{5} +2\sqrt{5}= 4\sqrt{5}\approx 8,94$ - является иррациональным

$\frac{x-9}{x-6}=\frac{3}{4}, \ \ \ x\neq6\\ \\ 4*(x-9)=3*(x-6)\\ \\ 4x-36-3x+18=0\\ x-18=0\\ x=18$

$(\frac{u}{v}+\frac{v}{u}+2)*\frac{uv}{v+u} = (\frac{u^2+v^2+2uv}{vu})*\frac{uv}{v+u} = \frac{(v+u)^2}{v+u} = v+u\\ v+u = 3\sqrt{2}+1+4-3\sqrt{2} = 5$