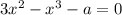
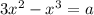
Рассмотрим две функции: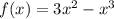 
и 
И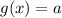зобразим на координатной плоскости график функции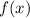 
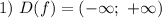
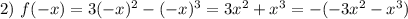
Функция 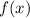не обладает свойством четности.
3) Находим абсциссы точек пересечения графика с осью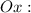 
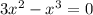
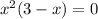
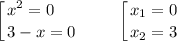
Находим ординату точки пересечения графика с осью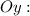 
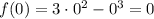
4) Находим производную:
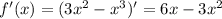
Критические точки:
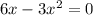
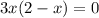
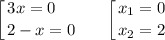
5) Составим таблицу (см. вложение).
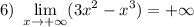
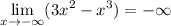
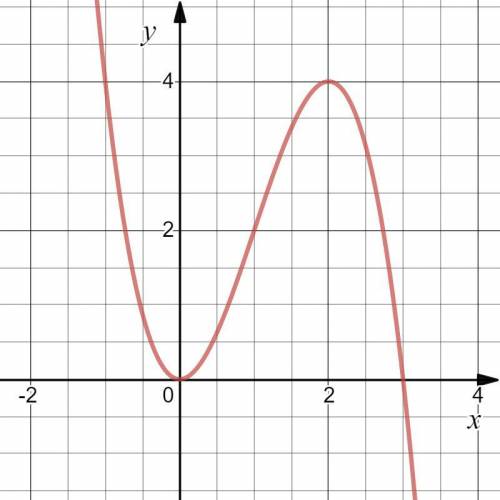
7) Используя результаты исследования, построим схематический график функции 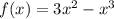(см. вложение).
Тогда уравнение 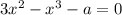будет иметь единственное решение, если графики функци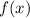й и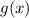 
будут иметь единственное пересечение.
Так произойдет, есл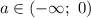и 
и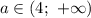 
ответ: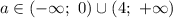 
Пусть х - цифра десятков;
у - цифра единиц .
По условию цифра десятков, увеличенная на 2, в 2 раза больше цифры единиц.
Исходя из этого, получаем первое уравнение:
х +2 = 2у
Ещё в условии сказано, что если цифры десятков и единиц поменять местами, то полученное число будет меньше первоначального на 27, т.е.
(10х+у) > (10у+х) на 27
Получаем второе уравнение:
(10х+у ) - (10у+х) = 27
Упростим это уравнение:
9х - 9у = 27
х - у = 3
Решаем систему:
{x + 2 = 2y
{x - y = 3
Из второго уравнения выразим х:
х = у + 3
Подставим в первое:
у + 3 + 2 = 2у
у = 5 - цифра единиц
х = 5 + 3
х = 8 - цифра десятков;
ответ: 85
2x - 7y = 3y
2x = 10y
X = 5y
X^4 + 5y^4 = ( 5y )^4 + 5y^4 = 625y^4 + 5y^4 = 630y^4
X^3y - x^2y^2 + xy^3 = ( 5y )^3•y - y^2•( 5y )^2 + y^3•5y = 125y^4 - 25y^4 + 5y^4 = 90y^4
630y^4 : 90y^4 = 7
ответ 7