Алгебра: Вычислить х (в квадрате) + у(в квадрате) , если ху=1, а х+у

Вычислить х (в квадрате) + у(в квадрате) , если ху=1, а х+у

👇

Увидеть ответ

Ответ:

Privet206

13.08.2020

X² + Y² = (X² + 2*X*Y + Y²) - 2*X*Y = (X + Y)² - 2*X*Y = 12² - 2*1 = 144 - 2 = 142

4,5(59 оценок)

Открыть все ответы

Ответ:

ЮкиНайи

13.08.2020

Нехай за год перший робітник виконає завдання, а за 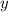год — другий. Тоді за одну годину перший робітник виконає $\dfrac{1}{x}$ усього завдання, а другий робітник — $\dfrac{1}{y}$ .

Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто 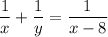$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{x-8}$

Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто 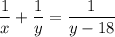$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{y-18}$

Складаємо систему з двох рівнянь:

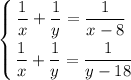
$\displaystyle \left \{ {{\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{x-8} \ } \atop {\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{y-18}}} \right.$

Тут 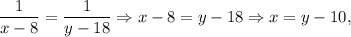$\dfrac{1}{x - 8} = \dfrac{1}{y - 18} \Rightarrow x - 8 = y - 18 \Rightarrow x = y - 10,$ оскільки ліві частини рівнянь рівні.

Підставимо 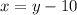x = y - 10 в перше рівняння:

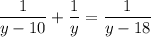
$\dfrac{1}{y - 10} + \dfrac{1}{y} = \dfrac{1}{y - 18}$

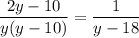
$\dfrac{2y - 10}{y(y-10)} = \dfrac{1}{y - 18}$

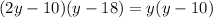
(2y - 10)(y - 18) = y(y - 10)

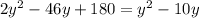
$2y^{2} - 46y + 180 = y^{2} - 10y$

$y^{2} - 36y + 180 = 0$

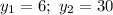
$y_{1} = 6; \ y_{2} = 30$

Якщо 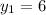$y_{1} = 6$ , то $x_{1} = 6 - 10 = -4$ — не відповідає сенсу задачі.

Якщо 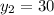$y_{2} = 30$ , то $x_{2} = 30 - 10 = 20$

Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.

Відповідь: 20 год і 30 год.

4,6(93 оценок)

Ответ:

данил20601

13.08.2020

1) tg x + 3/tg x = 4, ОДЗ tg x <> 0

множим уравнение на tg(x), который по ОДЗ не ноль

(tg x)^2 - 4 tg x + 3 = 0

видим здесь квадратное уравнение относительно tg x.

а ещё видим, что сумма показателей степеней равна 1-4+3 = 0, поэтому один корень =1, второй по т.Виетта =3

уравнение распадается на совокупность

tg x = 1

tg x = 3

выписываем решение:

x = arctg(1) + pi n, где ncZ

x = arctg(3) + pi k, где kcZ

ну можно ещё вспомнить, что arctg(1) = pi/4

2) вспоминаем формулу косинуса двойного угла:

cos 2a = 2 cos^2 a - 1

если a = x/2, то исходное уравнение может быть представлено как

cos x + 1 + sin x = 0

вобщем, тут уже очевидно, что либо cos x =0, sin x =-1, либо cos x=-1, sin x =0

но чтобы совсем честно решать, придётся поколдовать.

синус направо и всё в квадрат!

(cos x +1)^2 = sin^2 x

cos^2 x + 2 cos x + 1 = 1 - cos^2 x

2 cos^2 x + 2 cos x = 0

cos x (cos x + 1) = 0

произведение обращается в ноль если хотя бы один из множителей обращается в ноль. значит опять совокупность:

cos x = 0

cos x = -1

x = pi/2 + pi n , ncZ,

x = pi + 2pi k, kcZ

но тут небольшая грабля. чуть выше мы возводили к вадрат. а нулевому косинусу соответствуют два значения синуса: +1 и -1. и один из них нам не подходит.

вобщем, проверяем корни и убеждемся, что из первой последователности половина значений выпадает (pi/2 + 2pi n НЕ являются корями. а pi/2 + pi + 2pi n - удовлетворяют)

ответ

x = 3pi/2 + 2pi n , ncZ,

x = pi + 2pi k, kcZ

4,4(18 оценок)

Это интересно:

Хобби-и-рукоделие

06.06.2021

Как поместить яйцо в бутылку: советы и хитрости...

Семейная-жизнь

11.06.2020

Как прекратить воевать со своим братом или сестрой...

Компьютеры-и-электроника