sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(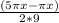
)cos(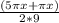
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
для начала выясним, если прибавить 11, то каждая из цифр ли увеличится на 11 или произойдет перенос разрядов. если произойдет перенос, то получится число вида Х0
для этого рассмотрим число Х0=10х=х^2-x*0+0^2=x^2, x=0, x=10
но если 10 получили прибавлением 11, то прибавляли не к двузначном числу. значит переноса не было
было число АВ=10а+b=a^2-ab+b^2
другое число CD=(A+1)(B+1)=10(a+1)+(b+1)=(a+1)^2-(a+1)(b+1)+(b+1)^2
a^2-ab+b^2+11=(a+1)^2-(a+1)(b+1)+(b+1)^2
a^2-ab+b^2+11=a^2+2a+1-ab-a-b-1+b^2+2b+1
a+b=10
выразим b=10-a и подставим:
10а+10-a=a^2-a(10-a)+(10-a)^2
9a+10=a^2-10a+a^2+100-20a+a^2
3a^2-39a+90=0
a^2-13a+30=0
(a-10)(a-3)=0
a=10 - между прочим, не цифра
а=3, b=10-3=7
число 37
после увеличения на 11 это 48
ответ: 37 и 48
пусть х-число десятков,у-число единиц
10х+у - двузначное число (х ≠0 )
по условию
10х+у=4(х+у)
10х+у=4х+4у
10х-4х=4у-у
6х=3у
у=2х
подставим вместо х числа от 1 и далее
получим двузначные числа : 12 ; 24; 36 ;48 - все они удовлетворяют данному условию
2.Если условие всё же НЕПОЛНОЕ,то оно выглядит так :
Найдите двузначное число,которое в 4 раза больше суммы его цифр и в 2 раза больше произведения его цифр.
пусть х-число десятков, у-число единиц
10х+у - двузначное число
запишем данные в задаче условия в виде системы :
{10x+y=4(x+y)
{10x+y=2xy
{10x+y=4x+4y
{10x+y=2xy
{6x=3y
{10x+y=2xy
{y=2x
{10x+2x=2x*2x
{y=2x
{12x=4x² так как х≠0,то поделим обе части на х ⇒⇒
{y=2x
{12=4x
{y=2x
{x=3 ⇒⇒ y=6
ответ : число 36.
( Возможны и другие варианты задания )