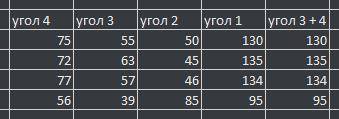
1) ∠2 = 180° - 75° - 55° = 50°
∠1 = 180° - ∠2 = 130°
∠3 + ∠4 = 130°
2) ∠2 = 180° - 135° = 55°
∠4 = 180° - 55° - 63° = 62°
∠3 + ∠4 = 135°
3) ∠3 = 180° - 77° - 46° = 57°
∠1 = 180° - 46° = 134°
∠3 + ∠4 = 134°
4) ∠4 = 180° - 39° - 85° = 56°
∠1 = 180° - 85° = 95°
∠3 + ∠4 = 95°
Объяснение:
Для начала надо знать что сумма всех углов любого треугольника равна 180 градусам, тогда всегда ∠ 2 + ∠ 3 + ∠ 4 = 180 градусам, а ∠ 1 внешний угол треугольника и всегда будет равен 180 - ∠ 2, а ∠ 3 + ∠ 4 ну это просто данное, так что сначала считаешь все углы и находишь одно из другого, а потом считаешь ∠ 3 + ∠ 4.
Итог:
1) ∠2 = 180° - 75° - 55° = 50°
∠1 = 180° - ∠2 = 130°
∠3 + ∠4 = 130°
2) ∠2 = 180° - 135° = 55°
∠4 = 180° - 55° - 63° = 62°
∠3 + ∠4 = 135°
3) ∠3 = 180° - 77° - 46° = 57°
∠1 = 180° - 46° = 134°
∠3 + ∠4 = 134°
4) ∠4 = 180° - 39° - 85° = 56°
∠1 = 180° - 85° = 95°
∠3 + ∠4 = 95°
И это такое посредственное доказательство что внешний угол в треугольнике равняется сумме двух других углов.
10x-8=-3x+5
10x+3x=5+8
13x=13
x=1
y(1)=10*1-8=10-8=2
(1;2) - точка пересечения графиков функций