y = x³ + 2x² + x + 3 [ - 3 ; - 0,5]
Найдём производную :
y' = (x³)' + 2(x²)' + (x)' + 3' = 3x² + 4x + 1
Приравняем производную к нулю :
3x² + 4x + 1 = 0
D = 4² - 4 * 3 * 1 = 16 - 12 = 4 = 2²
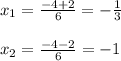
x= - 1/3 ∉ [- 3 ; - 0,5]
Сделаем рисунок и определим знаки производной на полученных промежутках :
+ -
[ - 3]___________[- 1]____________[- 0,5]
↑ ↓
max
На промежутке [- 3 ; - 1] функция возрастает, а на промежутке [- 1; - 0,5]- убывает . Значит в точке x = - 1 функция имеет максимум.
y (- 1) = (- 1)³ + 2 * (- 1)² - 1 + 3 = - 1 + 2 - 1 + 3 = 3
ответ : наибольшее значение функции равно 3
1) Строить график не буду, объяню как решать.
y = -x^2+4x - квадратичная функция
График - парабола, ветви вниз, т.к. перед x^2 отрицательный коэффициент.
Вершина параболы
x(0) = -b/2a = -4/2*(-1) = -4/-2 = 2
y(0) = 4
Таблица значений
x|0|1|2|3|4
y|0|3|4|3|0
Строишь по клеткам параболу.
а)
Значение функции = значение на оси Оу
На оси х находишь точки 0 и 3 проводишь пунктирную линию к графику.
Получается
у наиб = 3
y наим = 0
б) y возрастает на примежутке ( минус бесконечность; 2]
убывает на промежутке [2; +бесконечность);
в)4x^2 - x^2 < 0
4x^2 - x^2 = 0
3x^2 = 0
x^2 = 0
x = 0
x (0; + бесконечность)