Объяснение:
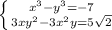
сложим эти два уравнения и преобразуем по формуле куба разности:
Для простоты вычислений введём константу С
![C=\sqrt[3]{5\sqrt{2}-7 }](/tpl/images/2018/3457/220b9.png)
C≈0,4142
Из последнего выражения имеем следующие тождества
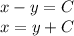
Подставляем x в первое уравнение
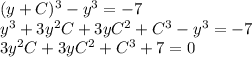
В последнее С³ подставим его значение, чтобы сократить семёрку.
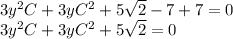
Теперь решаем обычное квадратное уравнение
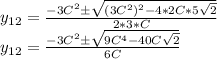
Тут получается что дискриминант отрицательный и корней нет.
Вариант второй, графический
из первого уравнения получаем график функции
![y=\sqrt[3]{x^{3} +7} \\](/tpl/images/2018/3457/4771c.png)
А из второго
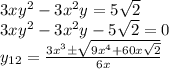
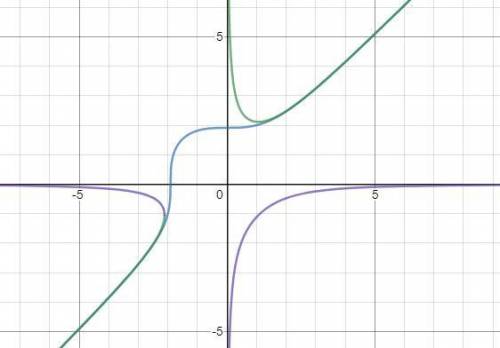
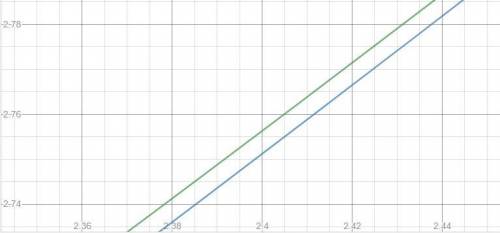
Строим графики.
Видим, что точек пересечения нет.
Графики стремятся приблизится друг к другу, но не пересекаются
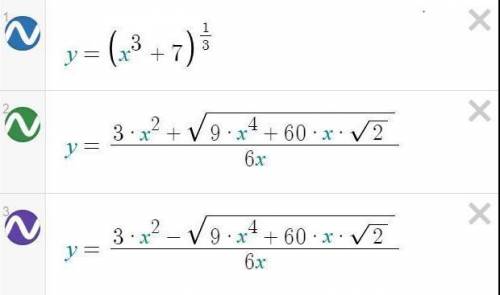
Наибольшая прибыль = 7 денежных единиц
Объяснение:
Пусть x - количество произведенной продукции П1, а y - количество произведенной продукции П2. Тогда цель задачи максимизировать значение (
) при условии ограничений на сырье и того, что нам надо произвести хоть что-то: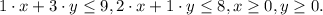 
Эти четыре неравенства задают заштрихованный под прямыми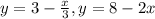 
четырехугольник в первом квадранте.
Значение максимизируемого выражения x+2y есть линии уровня z=x+2y, а так как градиент функции z(x,y) равный grad z = {1;2} направлен в сторону первого квадранта, то значения z будут тем больше, чем дальше мы продвинем линию уровня в первый квадрант. С учетом ограничений наибольшее значение изготовленной продукции придется на пересечение прямых, которые задают четырехугольник: 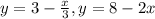. Точка пересечения (3;2). Значит, наибольшая прибыль, которую можно получить 3+2*2=7.
