1 фирма: 60000 деталей
2 фирма: 42000 деталей
Объяснение:
Задача на совместную работу!
A-работа (в данном случае - количество деталей)
t - время (в данном случае - в днях)
P - производительность (в данном случае - количества деталей в день)
P=A/t; t=A/P; A=P*t
Пусть первая фирма произвела х тысяч деталей, тогда вторая фирма произвела (102-x) тысяч деталей.
Производительность первой фирмы: P₁=x/30 (то есть х тыс. деталей за 30 дней)
Производительность второй фирмы: P₂=(102-x)/28 (тыс. деталей/дней)
Работа производимая первой фирмой за 6 дней:
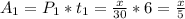 -тысяч деталей
-тысяч деталей
Работа производимая второй фирмой за 4 дня:
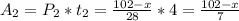 -тысяч деталей
-тысяч деталей
По условию: A₁-A₂=6 тыс. деталей
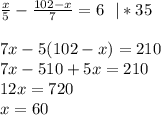
За х мы обозначали сколько тысяч деталей изготовила первая фирма.
Тогда вторая фирма изготовила: 102-x=102-60=42 тыс деталей
В решении.
Объяснение:
Решить неравенства:
1) 5х² - 7х - 6 > 0
Приравнять к нулю и решить как квадратное уравнение:
5х² - 7х - 6 = 0
D=b²-4ac =49 + 120 = 169 √D=13
х₁=(-b-√D)/2a
х₁=(7-13)/10
х₁= -6/10
х₁= -0,6;
х₂=(-b+√D)/2a
х₂=(7+13)/10
х₂=20/10
х₂=2.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -0,6 и х= 2, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у > 0 (как в неравенстве), при значениях х от - бесконечности до -0,6 и при х от 2 до + бесконечности.
Решение неравенства: х∈ (-∞; -0,6)∪(2; +∞).
Неравенство строгое, скобки круглые.
3) -х² - 2х - 6 >=0
Приравнять к нулю и решить как квадратное уравнение:
-х² - 2х - 6 =0/-1
х² + 2х + 6 =0
D=b²-4ac =4 - 24 = -20
D < 0
Уравнение не имеет действительных корней, так как парабола не пересекает ось Ох, а неравенство не имеет решения.
5) 5х² - 6 <= 0
Приравнять к нулю и решить как неполное квадратное уравнение:
5х² - 6 = 0
5х² = 6
х² = 6/5
х² = 1,2
х = ±√1,2
х₁ = √1,2 ≈ 1,1;
х₂ = -√1,2 ≈ -1,1.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -√1,2 (≈ -1,1) и х= √1,2 (≈ 1,1), отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (как в неравенстве), при значениях х от -√1,2 до х= √1,2.
Решение неравенства: х∈ [-√1,2; √1,2].
Неравенство нестрогое, скобки квадратные.
7) 5х² - х + 6 < 0
Приравнять к нулю и решить как квадратное уравнение:
5х² - х + 6 = 0
D=b²-4ac =1 - 120 = -119
D < 0
Уравнение не имеет действительных корней, так как парабола не пересекает ось Ох, а неравенство не имеет решения.
///////////////////////////////////////