7x²=21x
Перенести условия в левую часть
72=21
72−21=0
Простой фактор
72=21
7(2−3)=0
Разделите обе части уравнения на один и тот же член
7(2−3)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
2−3=0
=1
b=-3
=0
=−(−3)±√(−3)2−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
x=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
9x²=27x
Перенести условия в левую часть
92=27
9x^{2}=27x9x2=27x
92−27=0
Простой фактор
92−27=0
9x^{2}-27x=09x2−27x=0
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
Разделите обе части уравнения на один и тот же член
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
²−3=0
=1
=−3
=0
=−(−3)±√(−3)²−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
Решаем чисто аналитически:
Сначала найдем точки пересечения прямых (каждой с каждой), получим 3 точки, являющиеся вершинами треугольника.
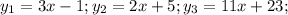
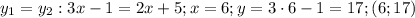 пусть это будет точка А.
пусть это будет точка А.
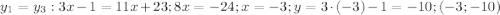 пусть это будет точка В.
пусть это будет точка В.
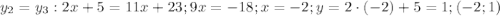 пусть это будет точка С.
пусть это будет точка С.
Итак, нашли координаты вершин треугольника.
Теперь вычислим расстояния между точками (от каждой до каждой)
Напомню, что расстояние между точками 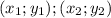
считается по формуле 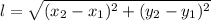
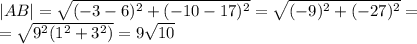
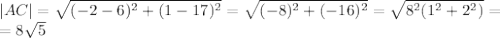
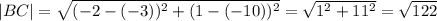
Известны длины всех сторон. По формуле Герона мы можем вычислить площадь. Но очень неприятно возиться с корнями, поэтому найдем лучше найти высоту треугольника, например, проведенной к основанию AC. Для этого надо вычислить коэффициенты уравнения прямой, содержащей эту высоту. Это можно сделать, исходя из того факта, что прямые BH (BH - высота к AC) и AC перпендикулярны, а значит, произведение их угловых коэффициентов равно -1.
Тогда уравнение прямой, перпендикулярной AC и проходящей через точку B, имеет вид
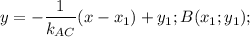
Надо понять, какое уравнение содержит точки A и C. Подставив в каждое координаты точек A и C, поймем, что это второе уравнение
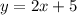
А учитывая, что B(-3;-10), получаем уравнение прямой, содержащей высоту к AC.
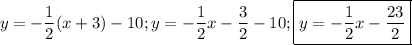
Теперь найдем координаты точки H - это пересечение прямой, содержащей высоту и прямой, содержащей точки A и C.
То есть
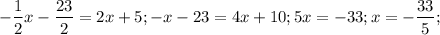
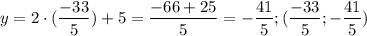
Вычислим длину высоты:
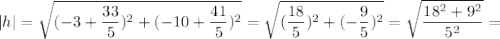
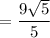
Площадь треугольника равна половине произведения основанию на высоту, проведенную к этому основанию. Считаем:
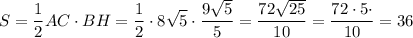
ответ: 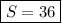
1/9 * 3^[3x]+3*3^[3x]-3^[3x]<57
3^[3x]+27*3^[3x]-9*3^[3x]<57
19*3^[3x]<57
3^[3x]<3
3x<1
x<1/3