1. ОТВЕТ: например,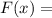 
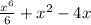, поскольку 
.
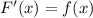Общий вид первообразных -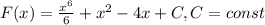 
2. Докажем, что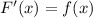 
:
.
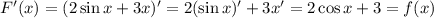Что и требовалось доказать.
3. Общий вид первообразных функции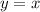 
- 
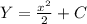, где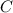 
- некоторое постоянное число. Если график первообразной проходит через точку 
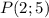, то это значит, что при подстановке 
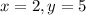получим верное равенство:
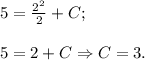
Искомая первообразная -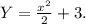 
ОТВЕТ: Y = x²/2 + 3.
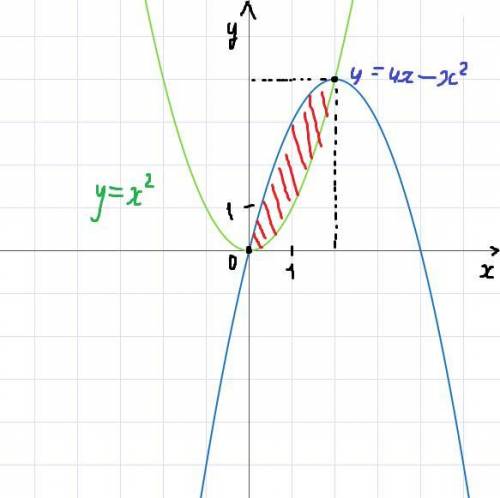
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.
Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид
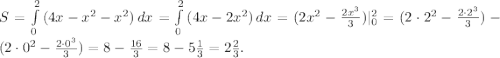
ОТВЕТ: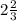 
кв. ед.
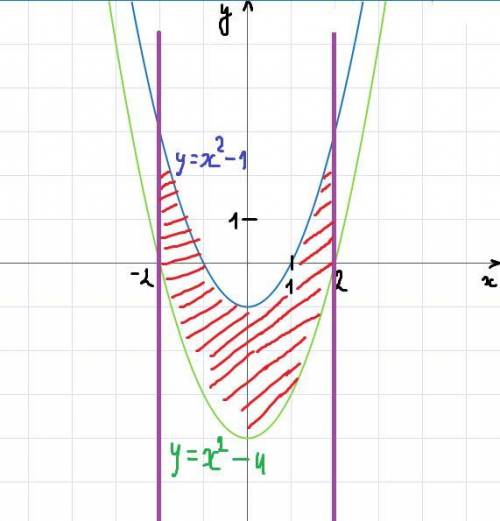
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.
Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид
![S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12](/tpl/images/1179/2526/6e4c7.png)
ОТВЕТ: 12 кв. ед.
6. Объем выполненной работы A(t) с момента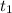 
по момент 
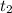согласно механическому смыслу определенного интеграла есть значение выражения интеграла
Имеем:
ОТВЕТ: ≈ 760.
2*3^n≤2^n+4^n
преобразуем
2 ≤ (2^n+4^n ) / 3^n = (2/3)^n +(4/ 3)^n
в правой части оба слагаемые положительные числа
первое слагаемое (2/3)^n - дробь -всегда меньше 1
второе слагаемое (4/3)^n - дробь -всегда больше 1
достаточное условие доказательства , чтобы одно из слагаемых было БОЛЬШЕ 2
рассмотрим n=1,2,3
n=1
(2/3)^1 +(4/ 3)^1 = 2/3+4/3=6/3 =2 <выполняется равенство 4/3 < 2
n=2
(2/3)^2 +(4/ 3)^2 = 4/9+16/9=20/9 =2+2/9 >2 <выполняется НЕравенство 16/9 < 2
n=3
(2/3)^3 +(4/ 3)^3 = 8/27+64/27=72/27 =2+18/27 <выполняется НЕравенство 64/27 > 2
второе слагаемое (4/3)^n > 2 , для всех 3 ≤ n
следовательно, для любого натурального n справедливо заданное неравенство
ДОКАЗАНО
Просто раскрываешь скобки. Первую по формуле, вторую правилом "фонтанчика" соблюдая знаки. Считаешь и получаешь - 7х+25
Дальше вместо икса подставляешь значение и получается - 8