Пусть число десятков двузначного числа равно х, а число единиц - у, тогда исходное число (10х + у).
Сумма его цифр равна 12:
х + у = 12, откуда
у = 12 - х.
Записанное в обратном порядке число будет (10у + х). По условию оно равно 4/7 от (10х + у), т.е.
(10у + х) = 4/7(10х + у)
или
7(10у + х) = 4(10х + у)
Подставим сюда у = 12 - х
7·(10·(12 - х) + х) = 4·(10х + 12 - х)
7·(120 - 10х + х) = 4·(9х + 12)
7·(120 - 9х ) = 4·(9х + 12)
840 - 63х = 36х + 48
99х = 792
х = 8 - число десятков исходного числа
у = 12 - х = 12 - 8 = 4 - число единиц исходного числа
исходное число 84, записанное в обратном порядке цифр число равно 48
ответ: эти числа: 84 и 48
пусть х грамм меди и у грамм цинка содержалось в первоначальном сплаве.
тогда х+у - масса первоначального сплава
по условию количество меди увеличилось на 40%, т.е. масса меди в новом сплаве равна х+0.4х=1.4х
по условию количество цинка уменьшилось на 40%, т.е. масса цинка в новом сплаве равна у-0.4у=0.6у
масса нового сплава тогда равна 1.4х+0.6у
также по условию в результате общая масса куска сплава увеличилась на 20% , т.е. масса нового сплава равна х+у+0.2(х+у)=1.2(х+у)
следовательно 1.4х+0.6у=1.2(х+у)
1.4х+0.6у=1.2х+1.2у
1.4х-1.2х=1.2у-0.6у
0.2х=0.6у
следовательно х=3у
процентное содержание меди в первоначальном сплаве равно х/(х+у)
т.к. х=3у то х/(х+у)=3у/(3у+у)=3у/4у=3/4= 0.75 или 75%
следовательно процентное содержание цинка равно 100%-75%=25%
ответ: меди - 75%, цинка - 25 %
Один из корней - делитель свободного члена. Перебираем делители -5 и находим, что подходит x=1. Делим уравнение на (x-1) (можно в столбик, можно по схеме Горнера):
(x-1)(x^2+5x+5)=0
Решаем второе уравнение как обычное квадратное, получаются корни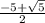 и
и 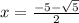
То есть всего у уравнения три корня: x=1,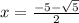 ,
,